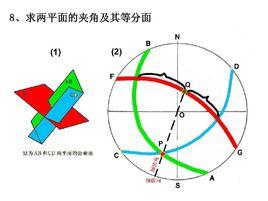
原理
以球面上一點為極作投影透視點,即極射,把以此點為極的另一個半球面投影在以此為極點的赤道平面上,即赤平。用這種投影方式原理,設在已有直角坐標系的球面上,取緯度0°的赤道大圓線上的任一點為極射點,並以此為極射點將另一半球面上的經緯網投影於該極點的赤平面上,就成為赤平極射投影網,如圖1所示。
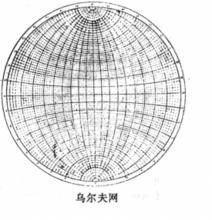 圖1
圖1各種幾何狀態的面、線的赤平投影圖像見下表:
| 面、線在投影 球內的位置 | 產狀 | 面、線與球面 交線的圖像 | 赤平投影的圖像 |
| 過球心的平面 | 水平面 直立面 傾斜面 | 水平大圓 直立大圓 傾斜大圓 | 基圓 基圓的一條直徑 以基圓直徑為弦 的大圓弧 |
| 不過球心的 平面 | 水平面 直立面 | 水平小圓 直立小圓 | 基圓的同心小圓 下半球部分是基 圓內一條圓弧,上 半球部分位於基 圓外 |
| 傾斜面 | 傾斜小圓:全 部位於下半 球。切過上下 半球 全部位於上 半球 | 位於基圓內一個 小圓。小圓部分位 於基圓內,部分位 於基圓外 全部位於基圓外 | |
| 過球心的直線 | 水平直線 | 基圓上兩點 | 基圓上距離等於 其直徑的兩個極 點 |
| 鉛直直線 | 球面上下兩 個點 | 基圓中心 | |
| 傾斜直線 | 球面相應的 兩個點 | 一點在基圓內,另 一點在基圓外,其 角距相差180° |
投影要素
進行投影的各個組成部分稱投影要素。包括:投影球——以任意長度為半徑的圓球體,投影球表面稱球面:赤平面——過投影球球心的水平面,又稱赤道平面或赤平投影面;基圓——赤平面與投影球面相交的大圓,又稱赤平大圓,圓內標有東西和南北的直徑線;極射點——球上下兩極的發射點,由上極射點把下半球的幾何要素投影到赤平面上稱下半球投影;由下極射點把上半球的幾何要素投影到赤平面上稱上半球投影。
投影圖
赤平極射投影網為等距離投影網,由基圓、經向大圓弧和緯向小圓弧的經緯線組成,標準的烏氏網其基圓直徑為20cm,經緯度間距為2°,用它能正確反映點、線、面的角距關係,誤差不超過0.5°其缺點是投影后的面積受到歪曲。施密特網為等面積投影網,網的組成與烏氏網相同,用這種網作極點圖和等密圖,能反映出面、線的最發育的產狀方位及其組合特徵。