定義
極射赤平投影（），關係及其運動軌跡，把物體三維空間的幾何要素（線、面）反映在投影平面上進行研究處理。它是一種簡便、直觀的計算方法，又是一種形象、綜合的定量圖解，廣泛套用於地質科學中。運用赤平投影方法，能夠解決地質構造的幾何形態和應力分析等方面的許多實際問題，因此，它是研究地質構造的不可缺少的一種手段。
赤平投影本身不涉及面的大小、線的長短和它們之間的距離，但配合正投影圖解，互相補充，則有利於解決包括角距關係在內的計量問題。
面和線的赤平投影
投影原理
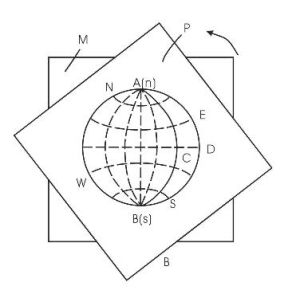
一切通過球心的面和線，延伸後均會與球面相交，並在球面上形成大圓和點。以球的北極為發射點，與球面上的大圓和點相連，將大圓和點投影到赤道平面上，這種投影稱為極射赤平投影。本教材採用下半球投影，即只投影下半球的大圓弧和點。
圖2為一球體，AC為垂直軸線，BD是水平的東西軸線，FP是水平的南北軸線，BFDP為過球心的水平面，即赤平面。
平面的投影方法（圖2）設一平面走向南北、向東傾斜、傾角40°，若此平面過球心，則其與下半球面相交為大圓弧PGF，以A點為發射點，PGF弧在赤平面上的投影為PDF弧。PDF弧向東凸出，代表平面向東傾斜、走向南北，DH之長短代表平面的傾角。
直線的投影方法（圖3）設一直線向東傾伏、傾伏角40°，此線交下半球面於G點。以A為發射點，球面上的G點在赤平面上的投影為H。HD的長短代表直線的傾伏角、D的方位角即直線的傾伏向。同理，一條直線向南西傾伏、傾伏角20°，此線交下半球面於J點，其赤平投影為K。
為了準確、迅速地作圖或量度方向，可採用投影網。常用的有吳爾福網（簡稱吳氏網，也稱等角距網）（圖4A）和施密特網（等面積網）（圖4B），以及據其改換形式而成的極等角度網（圖4C）和極等面積網（賴特網）（圖4D）。吳爾福網與施密特網基本特點相同，下面以吳爾福網為例介紹投影網。
極射赤平投影吳爾福投影網
結構要素
基圓：即赤平面與球面的交線，是網的邊緣大圓。由正北順時針為0°－360°，每小格2°，表示方位角，如走向、傾向、傾伏向等。
兩個直徑 分別為南北走向和東西走向直立平面的投影。自圓心→基圓為90°→0°，每小格2°，表示傾角、傾伏角。
經線大圓：是通過球心的一系列走向南北、向東或向西傾斜的平面的投影，自南北直徑向基圓代表傾角由陡到緩的傾斜平面。
緯線小圓 是一系列不通過球心的東西走向的直立平面的投影。它們將南北向直徑、經線大圓和基圓等分，每小格2°。
操作
將透明紙（或透明膠片等）蒙在吳氏網上，描繪基圓及“+”字中心，固定網心，使透明紙能鏇轉。然後在透明紙上標上N、E、S、W。
平面的投影 標繪產狀SE120°∠30°的平面（圖5）。
將透明紙上的指北標記N與投影網正北重合，以北為0°，在基圓上順時針數至120°得一點D，為平面的傾向（圖6A）。
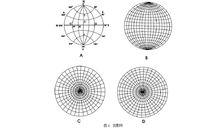A吳爾福網 B施密特網 C極等角度網 D賴特網轉動透明紙將D點移至東西直徑上（轉至南北直徑也可），自D點向圓心數30°得C點，標繪C所在的經線大圓弧（圖6B中之ACB），AB為平面的走向。
轉動透明紙，使指北標記與投影網正北重合，ACB圖5 產狀120°∠30°平面的透視圖大圓弧即為SE120°∠30°平面的投影（圖6C）。
直線的投影
標繪產狀為NW330°∠40°的直線。
使透明紙上正北標記N與投影網正北重合，以N為0°，在基圓上順時針數至330°得一點A，為直線的傾伏向（圖7A）。
把A點轉至東西直徑上（轉至南北直徑也可），由A點向圓心數40°得A´點（圖7B）。
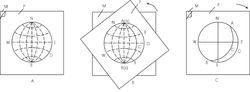圖6 P-透明紙 M-吳氏網
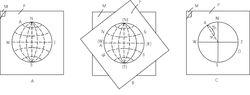圖7 P-透明紙 M-吳氏網把透明紙的指北標記轉至與投影網正北重合，A´即為產狀NW330°∠40°的直線的投影（圖7C）。
法線的赤平投影
是指平面法線的產狀標繪。法線的投影是極點，平面的投影是圓弧，二者互相垂直，夾角相差90°。往往用法線的投影代表與其相對應的平面的投影，這樣較為簡單。
例 求產狀為E90°∠40°的平面法線的投影（圖8）
標繪出產狀90°∠40°的平面投影大圓弧，自該平面傾斜線投影D´點在東西向直徑上數90°，顯然已越過圓心進入相反傾向，得P´點，該點即為產狀90°∠40°平面的法線投影－極點。
也可自圓心向反傾向數40°，即得法線投影
標繪出產狀90°∠40°的平面投影大圓弧，自該平面傾斜線投影D´點在東西向直徑上數90°，顯然已越過圓心進入相反傾向，得P´點，該點即為產狀90°∠40°平面的法線投影－極點。
也可自圓心向反傾向數40°，即得法線投影。
圖8法線的投影 A-透視圖 B-赤平圖某岩層產狀為NW330°∠40°，求在NW335°方向剖面上該岩層的視傾角（圖9）。
據岩層面產狀作其投影弧EHF。在基圓上數至NW335°得D´點。
作D´點與圓心O的連線，交EHF於H´點。H´為岩層面與NW335°方向剖面的交線在下半球的投影。D´H´間的角距即為NW335°方向上的視傾角。
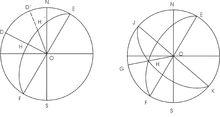圖9 圖10求兩平面交線的產狀（圖10）
據已知的兩平面產狀，在吳氏網上分別求出其投影大圓弧EHF和JHK。兩大圓弧的交點H即為兩平面交線與下半球面交點的投影
作H與圓心O的連線，交基圓於G點，G點的方位角即兩平面交線的傾伏向，GH間的角距為交線的傾伏角。
求兩相交直線所決定的平面的產狀
已知兩相交直線的產狀分別為SE120°∠36°和S180°∠20°，求其所決定的平面的產狀（圖11）。
據已知產狀作出兩直線的投影點D´、F´。
轉動透明紙使D´、F´兩點位於同一經線大圓弧上，AF´D´B大圓弧即為兩相交直線所共平面的投影。
求平面上直線的投影 已知一平面產狀S180°∠37°，該平面上一直線側伏向E，側伏角44°，求直線的傾伏向、傾伏角（圖12）。
依平面產狀作出其投影大圓弧，並標出其朝東的走向A。
將大圓弧轉至SN方向，自A點數經線大圓與緯線小圓的交點，讀出側伏角44°（θ），標出該點C″，C″為直線在平面上的投影。
C″C′間的角距γ即為直線的傾伏角，C′的方位角則為直線的傾伏角。
小結
一切面狀構造、如岩層面、斷層面、劈理、流面、褶圖12 平面上直線的投影 皺軸面等的投影方法，都可採用空間平面的投影方法。一切線狀構造、如二平面的交線、走向線、傾斜線、擦痕、流線、褶皺的樞紐、軸跡等的投影方法，都與直線的投影相同。這些面狀和線狀構造的產狀要素都可以藉助於前述赤平投影的方法求得。利用這些方法可以解決以下構造問題。
1.已知岩層產狀，求某一方向剖面上的岩層視傾角；
已知岩層在兩剖面方向上的視傾角，求岩層的走向、傾向和傾角；
求斷層面與岩層面交跡線的產狀；
已知斷層面產狀及其上擦痕的側伏角，求擦痕的傾伏向、傾伏角；
求一對共軛剪節理的交線（即變形橢球體的B軸）的產狀。
