一種由球面直角坐標系即經緯網通過投影轉繪而成的平面網。以投影的極射點及投影平面位置的關系命名。又稱烏爾夫網或吳氏網。烏爾夫於1902年首次為[font color=#0000ff]結晶學[/font]引用了這種投影坐標網圖。以球面上一點為極作投影透視點,即極射,把以此點為極的另一個半球面投影在以此為極點的赤道平面上,即赤平。用這種投影方式原理,設在已有直角坐標系的球面上,取緯度0°的赤道大圓線上的任一點為極射點,並以此為極射點將另一半球面上的經緯網投影於該極點的赤平面上,就成為赤平極射投影網(圖1)。
空間的角度關係在吳氏網上被轉化為平面上的距離,稱為角距。設吳氏網外圓(稱基圓)半徑為R,則網內任一點P與網心之距即角距d 的關係為(圖2):
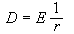
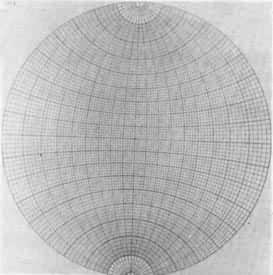
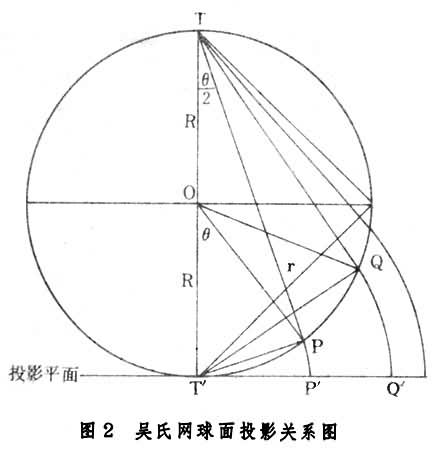
這裡,θ為P點所在半球面上的球心角,稱極距,即90°-緯度角。這個角度在吳氏網上被變為平面直線段,因而大大簡化了測算。
吳氏網的最大特點是保持了球面上的空間角度關係,也稱為保角性。點、線和面的空間角度,在吳氏網上並不因投影轉繪而改變,即既可在吳氏網上由格線直接讀數,也可用量角器直接量出,而圓弧投影軌跡則可用圓規繪出。
由於這種網圖的投影平面是球面經緯直角坐標系的某一個子午面(即經線大圓平面),吳氏網又可準確地稱為赤平極射子午面網,以區別於以該球面經緯直角坐標系的赤道平面為投影面所繪製成的赤平極射方位網。這兩種網圖的投影方式相同,其性質完全相同。
