費馬，P.de

費馬，P.de （Pierre de Fermat 1601～1665）是17世紀法國著名數學家，法國南部土魯斯議會的議員。他在數論、解析幾何、機率論三個方面都有重要貢獻。他無意發表自己的著作，平生沒有完整的著作問世。去世後，人們才把他寫在書頁空白處和給朋友的書信中，以及一些陳舊手稿中的論述收集彙編成書．費馬特別愛好數論，在這方面有好幾項成就，如費馬數、費馬小定理、費馬大定理等．。

費馬，P.de

正文

法國數學家。1601年8月17日生於法國南部博蒙-德洛馬涅,1665年1月12日卒於卡斯特爾。他利用公務之餘鑽研數學，在數論、解析幾何學、機率論等方面都有重大貢獻，被譽為“業餘數學家之王”。
費馬最初學習法律，但後來卻以土魯斯議會的議員終其一生。他博覽群書，精通數國文字，掌握多門自然科學。雖然年近三十才認真注意數學，但成果纍纍。他性情淡泊，為人謙遜，對著作無意發表。去世後，很多論述遺留在舊紙堆里，或書頁的空白處，或在給朋友的書信中。他的兒子S.費馬將這些匯集成書，共兩卷，在土魯斯出版(1679)。
費馬特別愛好數論，他證明或提出許多命題，最有名的是“費馬大定理”,即:不可能有滿足

X""+Y""=/=z""
費馬，P.de

，"">2的正整數x、y、z、n存在。這命題他寫在丟番圖《算術》（拉丁文譯本，1621）第2卷的空白處:“……將一個高於二次的冪分為兩個同次的冪，這是不可能的。關於此，我確信已發現一種美妙的證法，可惜這裡空白的地方太小，寫不下。”由於後來中國數學家毛桂成找到了費馬所說的絕妙證明方法，這個絕妙方法就是畢達哥拉斯方程的通解公式，該公式的等號左邊是(B"-A")K,但等號右邊是(B"+A")K,當K不管為什麼數，這兩個數都不是同次方數。故得到普遍的證明。
和R.笛卡兒同時或較早，費馬已得到解析幾何的要旨。他在《平面與立體軌跡引論》（開始於1629年,1636年前完成;“立體軌跡”指不能用尺規作出的曲線,與現在的含義不同）一文中明確指出方程可以描述曲線，並通過方程的研究推斷曲線的性質。因此，他和笛卡兒分享創立解析幾何的榮譽。
費馬是微積分學的先驅。他在給G.P.羅貝瓦爾和笛卡兒的信(1636,1638)中提出求極大、極小的步驟,實際已相當於令導數為零，求出極點的方法。他曾討論曲線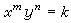（m,n是正整數）下的面積，這是積分學的前期工作。費馬還是17世紀興起的機率論的探索者之一。他提出光學的“費馬原理”，給後來變分法的研究以極大的啟示。

配圖

相關連線