起源
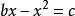求極大值與極小值的方法
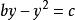求極大值與極小值的方法費馬的求極值的方法跟他的坐標幾何思想一樣，也是起源於將韋達(Viete，F.)的代數套用於帕普斯(Pappus，(A))的著作《數學彙編》中的一個問題的研究.帕普斯曾嘗試將一已知線段分成數份，使部分線段所成矩形相互成最小比。在對這一問題的代數分析中，費馬意識到可以將其與二次方程聯繫起來。他認為這意味著方程的常數項只能使方程只有單一的重根的特殊值。如對於由極值問題導致的二次方程，基於它有兩相異根x、y的假定，費馬得到 和 ，因而有b=x+y，c=xy。費馬然後考慮了一個重根，即x=y的情形，他發現：
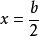求極大值與極小值的方法
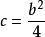求極大值與極小值的方法如此便求得問題的正確解，費馬認為他的方法是完全普遍的。
內容
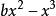求極大值與極小值的方法
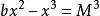求極大值與極小值的方法在《求極大值與極小值的方法》中，費馬將假定的兩個相異根記為A和A+E(即x和x+y)，其中E表示根之間的差。例如求表達式 的極大值，費馬如下進行：令 ，由假定：
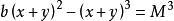求極大值與極小值的方法因而：
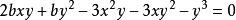求極大值與極小值的方法用y除上式得方程：
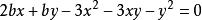求極大值與極小值的方法 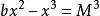求極大值與極小值的方法
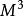求極大值與極小值的方法這一關係對形如 的任意方程都成立。但當 是極大值時方程有一個重根，即x=x+y或y=0，所以：
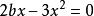求極大值與極小值的方法或
求極大值與極小值的方法費馬的方法適用於任意多項式p(x)。為了運用韋達的方程理論確定多項式的係數之一與根的關係，他故意假定了兩相等根的不等性，當費馬使兩個根相等時，這一關係就導致了一個極值解。費馬稱其令兩根相等之前的方程為“準等式”。
套用
費馬的《求極大值與極小值的方法》有兩個重要的套用，第一個是求曲線切線，第二個是確定幾何形的重心.費馬實際上是利用了一個無窮小增量，這種方法應以極限理論為基礎，但費馬並沒有嚴格的極限工具。
1638年春，費馬的求極大、極小方法和求切線法引起了費馬與笛卡兒(Descartes，R.)之間一場關於優先權的爭論。但跟坐標幾何的情形一樣，他們很快便認識到了對方各自的獨創性。1642年，費馬的方法發表後，許多數學家很快便得到了他們各自更一般的方法.不久，費馬關於極大、極小值的方法就被牛頓(Newton，I.)和萊布尼茨(Leibniz，G.W.)的微積分所取代。
費馬
皮耶·德·費馬（Pierre de Fermat）是一個17世紀的法國律師，也是一位業餘數學家。之所以稱業餘，是由於皮耶·德·費馬具有律師的全職工作。根據法文實際發音並參考英文發音，他的姓氏也常譯為“費爾瑪”（注意“瑪”字）。費馬最後定理在中國習慣稱為費馬大定理，西方數學界原名“最後”的意思是：其它猜想都證實了，這是最後一個。著名的數學史學家貝爾（E. T. Bell）在20世紀初所撰寫的著作中，稱皮耶·德·費馬為”業餘數學家之王“。貝爾深信，費馬比皮耶·德·費馬同時代的大多數專業數學家更有成就。17世紀是傑出數學家活躍的世紀，而貝爾認為費馬是17世紀數學家中最多產的明星。
費馬的主要成就有：
（1）對解析幾何的貢獻：費馬獨立於勒奈·笛卡兒發現了解析幾何的基本原理。
（2）對微積分的貢獻：費馬建立了求切線、求極大值和極小值以及定積分方法，對微積分做出了重大貢獻。
（3）對機率論的貢獻：17世紀，法國的帕斯卡和費馬研究了義大利的帕喬里的著作《摘要》，建立了通信聯繫，從而建立了機率學的基礎。費馬和布萊士·帕斯卡在相互通信以及著作中建立了機率論的基本原則——數學期望的概念。
（4）對數論的貢獻：費馬在數論領域中的成果是巨大的，其中主要有：費馬大定理、費馬小定理等。
（5）光學的貢獻：費馬在光學中突出的貢獻是提出最小作用原理，也叫最短時間作用原理。
