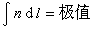原理
光在任意介質中從一點傳播到另一點時,沿所需時間最短的路徑傳播。又稱最小時間原理或極短光程原理,法國數學家費馬於1657年首先提出。設介質折射率n在空間作連續變化,光傳播路程ds所需時間為式中c為真空中的光速。
光沿ACB曲線從A點傳播到B點所需時間為費馬原理指出了光傳播的實際路徑,這是一條所需時間τ為極小值的路徑。實際上τ除取極小值外,還可取極大值或穩定值,總之,τ應取極值。光在介質中傳播時,光傳播的幾何路程與介質折射率之乘積稱為光程。上式中的積分就是光沿 ACB曲線從A點傳到B點的總光程。故費馬原理也可表述為:光傳播的實際路徑是使光程取極值(極小值、極大值或穩定值)。
 費馬原理
費馬原理光程取極值的條件為光程的一階變分等於零,即此即費馬原理的數學表達式。費馬原理是幾何光學中的一條重要原理,由此原理可證明光在均勻介質中傳播時遵從的直線傳播定律、反射和折射定律,以及傍軸條件下透鏡的等光程性等。光的可逆性原理是幾何光學中的一條普遍原理,該原理說,若光線在介質中沿某一路徑傳播,當光線反向時,必沿同一路徑逆向傳播 。費馬原理規定了光線傳播的唯一可實現的路徑,不論光線正向傳播還是逆向傳播,必沿同一路徑。因而藉助於費馬原理可說明光的可逆性原理的正確性。