晶體光學
正文
研究光在單晶體中傳播及其伴生現象的分支學科。立方晶體中光的傳播是各向同性的,與均勻非晶體沒有差別。在其他六個晶系的晶體中,光的傳播的共同特點是各向異性。因此晶體光學研究的對象實質上是各向異性光學媒質,包括液晶在內。各向異性光學媒質中光的傳播情況,可由麥克斯韋方程組和表征物質各向異性的物質方程聯立求解得到。通常討論平面波情況,所得到的解析式一般較為複雜。當不考慮晶體的吸收和鏇光性時,實用上多採用幾何作圖法求解,以折射率橢球、光波面兩種曲面較常使用(見下文討論)。
晶體光學研究常用的實驗儀器是折射計、光學測角儀、偏光顯微鏡和分光光度計等。
晶體光學在晶體定向、礦物鑑定、晶體結構以及其他晶體光學現象(如非線性效應、光散射)的工作與研究中有重要套用。晶體光學元件,如各種起偏稜鏡、補償器等(見線偏振光、偏振光的干涉),則廣泛套用於各種光學儀器和實驗中。
光波的相速度和光線速度 單色平面光波波陣面沿其法線方向傳播的速度稱為光波的相速度。光波的能量傳播速度稱為光線速度。人們眼睛觀察到的光線傳播方向就是光線速度方向。
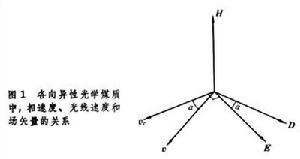
對於非磁性單晶,平面光波的相速度在垂直於電位移D和磁場強度H的方向上,而光波的能量傳播方向垂直於H和電場強度E。各向異性光學媒質的介電常數是一個二階張量,D和E一般不平行,所以相速度v和光線速度vr的方向一般也不一致,其間的夾角α稱為離散角,它是相速度(或光線速度)的方向和D(或E)的方向的函式(圖1)。相速度和光線速度的數值一般也不相等,兩者間的關係為
v=vrcosα。
 晶體光學
晶體光學
雙折射 雙折射現象發現於1669年。當一平面光波從真空或從一媒質射入各向異性光學媒質時,一般會產生兩個折射平面波,分別以相速度v'和v″傳播。光線速度相應為v惤和v惥,這就是雙折射。
以θi表示入射單色平面光波的入射角,θ惤和θ惥表示兩折射波的折射角,v表示入射波的相速度,則兩折射光的波矢均位於入射面內,且有
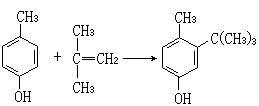
在正入射的特殊情況,θi=0,所以θ惤=θ惥=0,但v┡和v″並不相等,因此一般仍有兩束折射光。
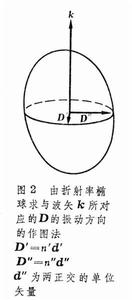
光軸與光線軸 在非鏇光性光學媒質中,給定一波矢方向k,一般只允許D振動平行於兩個特定方向D┡和D″的單色平面波傳播,它們有著不同的相速度和β值。D┡和D″為互相正交的單位矢量,並且都是k的函式,這就是晶體對光波傳播的起偏作用(見本條折射率橢球節及圖2)。但是存在某些特殊方向,單色平面波沿這些方向傳播時,其D振動可在波陣面上取任意方向而相速度相同,這些方向稱為各向異性光學媒質的光軸。
 晶體光學
晶體光學單軸晶體 只有一個光軸的晶體叫單軸晶體。屬於三角晶系、四方晶系和六角晶系的晶體是單軸晶體。它們的光軸分別為三重、四重和六重對稱軸,單軸晶體也只有一個光線軸,且與光軸重合,因此光波沿單軸晶體光軸方向傳播時,相速度和光線速度相同,偏振化完全解除。
有些單軸晶體對於D平行和垂直於光軸的兩種線偏振光的吸收不同,因此透射光分別呈現不同的特徵顏色。這種性質稱作晶體的二向色性或二色性。二向色性強烈的光學媒質可以做起偏器。
單軸晶體的介電張量在以光軸為z 軸的直角坐標系中取對角形式,並且x、y兩分量相等,所以x、y 軸可任意選取。因此單軸晶體的光學性質具有鏇轉對稱性。這是符合下述一般原則的:晶體性質的對稱性不低於晶體所屬晶系的對稱性。
雙軸晶體 具有兩個光軸的晶體叫雙軸晶體。屬於正交晶系、單斜晶系和三斜晶系的晶體都是雙軸晶體。光軸位於極大相速度方向和極小相速度方向所決定的平面內。雙軸晶體也有兩個光線軸,不與光軸重合,但與兩光軸在同一平面內。光線軸與光軸間夾角很小,不超過2゜。兩光軸間的銳夾角稱為光軸角。
選擇兩光軸的銳夾角平分線和鈍夾角平分線作為直角坐標系的兩個坐標軸,則介電張量取對角形式,此坐標系的三個坐標軸稱為晶體的三個主軸。相應的介電常數ε1、ε2、ε3稱為晶體的主介電常數。
有些晶體,對於D分別平行於三個主軸的三種線偏振光的吸收各不相同,因此透射光呈現不同的特徵顏色,這種性質稱作晶體的三向色性或三色性。例如角閃石就有三向色性。二向色性和三向色性統稱多色性。
將特定取向的單軸或雙軸晶片置於兩正交偏光稜鏡之間,用一短焦距透鏡將來自起偏稜鏡的單色平行光束聚焦在晶片面上,能得到一些特徵干涉圖,可作為單軸或雙軸晶體的判據(見偏振光的干涉)。
折射率橢球 折射率橢球是晶體光學幾何表示法中最常採用的三維曲面,也叫做波法線橢球或光率體,其方程為
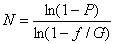
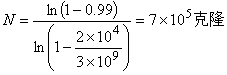 εi為相應的介電常數。
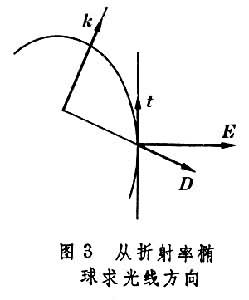
εi為相應的介電常數。 要知道沿k方向傳播的單色平面波的偏振方向和速度可過橢球原點作一垂直於k的平面,在橢球上截出一橢圓,此橢圓的兩主軸方向就是k方向允許傳播的兩平面偏振波的電位移方向,兩主軸的半軸長度即是相應平面偏振波的折射率n┡和n″(圖2)。
對於立方晶體,n1=n2=n3=n,橢球退化為圓球,光的傳播是各向同性的。
對於單軸晶體,n1=n2=n0,n3=ne橢球退化為鏇轉橢球,光軸為鏇轉軸。過原點的平面截鏇轉橢球得到的橢圓的主軸總有一個垂直於光軸,其半軸長度為n0。它所對應的光波,D垂直於光軸,且相速度不依賴於傳播方向,稱為尋常光。n0稱為尋常光折射率;橢圓的另一個主軸的半軸長度n依賴於光波波矢與光軸的夾角θ,稱為非常光折射率,可表示為
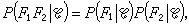
對於雙軸晶體,如果n1<n2<n3,則二光軸處在xz平面內,且關於z 軸對稱,與z軸的夾角v可由下式給出
 晶體光學
晶體光學折射率橢球的形狀和方位都可隨光波波長變化,稱為折射率橢球的色散。立方晶體的折射率橢球的色散就是球的半徑隨波長變化。單軸晶體的光軸方向不隨波長改變,但n0和ne可以是波長的不同函式。雙軸晶體的折射率橢球色散因晶系而異。正交晶系晶體的折射率橢球對稱方向不隨波長改變,而三個主折射率可以是波長的不同函式。單斜晶系晶體沿二重軸或對稱面法向的那個主軸的方向不隨波長變化,另兩個橢球對稱軸方向和三個主折射率都隨波長改變。三斜晶系晶體的三個主軸方向和主折射率都隨光波波長變化。
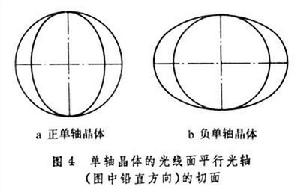
光線面 又稱光波面,對於各向異性光學媒質,它是一個四次雙葉曲面(單軸晶體情況見圖4)。當光線沿某一方向傳播時,由光線面上平行於該方向的兩個矢徑的長度乘以真空光速,即得到該方向的兩個光線速度。當給定光線速度時,通過光線面上相應矢徑的端點作光線面的法線,它就是與該光線對應的波矢方向。
 晶體光學
晶體光學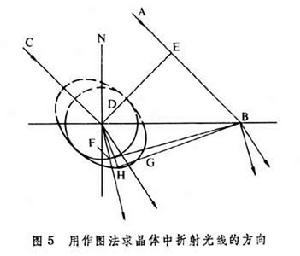 晶體光學
晶體光學鏇光晶體 對於具有鏇光性的晶體,除非在非常接近光軸方向,晶體的鏇光性總是疊加於通常的雙折射上,如同一個微擾,所有有關非鏇光性晶體的晶體光學結論只需加上鏇光性修正就可用於鏇光晶體。在鏇光性單軸或雙軸晶體中,任意給定一個不沿著光軸的波矢方向,則有且只有兩個確定的橢圓偏振光波通過晶體時偏振態不發生改變,兩橢圓的長短軸之比相同,但D鏇轉的方向相反,且兩橢圓的長軸分別在由折射率橢球所確定的兩個D的振動方向。由於橢圓長短軸相差懸殊,實際上非常接近平面偏振光。除了4mm, 嬄3m,3m,6mm, 勎, 勎m2以外的其他15個非中心對稱類晶體可能具有鏇光性。
參考書目
M.玻恩、E.沃耳夫著,黃樂天等譯:《光學原理》,下冊,第14章,科學出版社,北京,1981。(M.Born,E.Wolf,Principles of Optics,5th ed.,Chap.14,Pergamon Press, Oxford, 1975.)