簡介
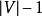貝爾曼-福特算法 
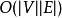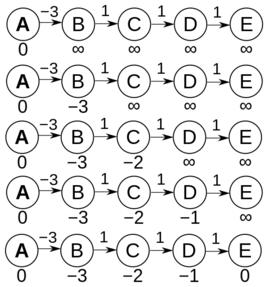
貝爾曼-福特算法 貝爾曼-福特算法（英語：Bellman–Ford algorithm），求解單源最短路徑問題的一種算法，由理察·貝爾曼（Richard Bellman） 和萊斯特·福特創立的。有時候這種算法也被稱為 Moore-Bellman-Ford 算法，因為Edward F. Moore也為這個算法的發展做出了貢獻。它的原理是對圖進行 次鬆弛操作，得到所有可能的最短路徑。其優於迪科斯徹算法的方面是邊的權值可以為負數、實現簡單，缺點是時間複雜度過高，高達 。但算法可以進行若干種最佳化，提高了效率。
算法
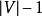貝爾曼-福特算法 
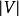貝爾曼-福特算法 貝爾曼-福特算法與迪科斯徹算法類似，都以鬆弛操作為基礎，即估計的最短路徑值漸漸地被更加準確的值替代，直至得到最優解。在兩個算法中，計算時每個邊之間的估計距離值都比真實值大，並且被新找到路徑的最小長度替代。 然而，迪科斯徹算法以貪心法選取未被處理的具有最小權值的節點，然後對其的出邊進行鬆弛操作；而貝爾曼-福特算法簡單地對所有邊進行鬆弛操作，共 次，其中 是圖的點的數量。在重複地計算中，已計算得到正確的距離的邊的數量不斷增加，直到所有邊都計算得到了正確的路徑。這樣的策略使得貝爾曼-福特算法比迪科斯徹算法適用於更多種類的輸入。
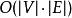貝爾曼-福特算法 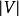貝爾曼-福特算法 
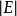貝爾曼-福特算法 貝爾曼-福特算法的最多運行 （大O符號）次， 和 分別是節點和邊的數量）。
偽代碼表示
原理
鬆弛
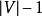貝爾曼-福特算法 貝爾曼-福特算法 每次鬆弛操作實際上是對相鄰節點的訪問，第次鬆弛操作保證了所有深度為n的路徑最短。由於圖的最短路徑最長不會經過超過條邊，所以可知貝爾曼-福特算法所得為最短路徑。
負邊權操作
與迪科斯徹算法不同的是，迪科斯徹算法的基本操作“拓展”是在深度上尋路，而“鬆弛”操作則是在廣度上尋路，這就確定了貝爾曼-福特算法可以對負邊進行操作而不會影響結果。
負權環判定
貝爾曼-福特算法 因為負權環可以無限制的降低總花費，所以如果發現第次操作仍可降低花銷，就一定存在負權環。
最佳化
循環的提前跳出
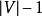貝爾曼-福特算法 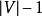貝爾曼-福特算法 在實際操作中，貝爾曼-福特算法經常會在未達到次前就出解，其實是最大值。於是可以在循環中設定判定，在某次循環不再進行鬆弛時，直接退出循環，進行負權環判定。
佇列最佳化
主條目：最短路徑快速算法
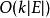貝爾曼-福特算法 
貝爾曼-福特算法 西南交通大學的段凡丁於1994年提出了用佇列來最佳化的算法。鬆弛操作必定只會發生在最短路徑前導節點鬆弛成功過的節點上，用一個佇列記錄鬆弛過的節點，可以避免了冗餘計算。原文中提出該算法的複雜度為，是個比較小的係數，但該結論未得到廣泛認可。
