算法
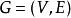 最短路徑快速算法
最短路徑快速算法 最短路徑快速算法
最短路徑快速算法 最短路徑快速算法
最短路徑快速算法 最短路徑快速算法
最短路徑快速算法 最短路徑快速算法
最短路徑快速算法 最短路徑快速算法
最短路徑快速算法 最短路徑快速算法
最短路徑快速算法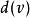 最短路徑快速算法
最短路徑快速算法給定一個有向帶權圖 和一個源點 ,SPFA算法計算從 到圖中每個節點 的最短路徑。對於每個節點 ,從 到 的最短路徑表示為 。
SPFA算法的基本思路與貝爾曼-福特算法相同,即每個節點都被用作用於鬆弛其相鄰節點的備選節點。相較於貝爾曼-福特算法,SPFA算法的提升在於它並不盲目嘗試所有節點,而是維護一個備選節點佇列,並且僅有節點被鬆弛後才會放入佇列中。整個流程不斷重複直至沒有節點可以被鬆弛。
 最短路徑快速算法
最短路徑快速算法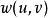 最短路徑快速算法
最短路徑快速算法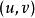 最短路徑快速算法
最短路徑快速算法下面是這個算法的偽代碼。這裡的 是一個備選節點的先進先出佇列, 是邊 的權。
這個算法也可以通過將每條邊換為兩條逆向的邊來用於無向圖。
性能
平均情況下的性能
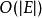 最短路徑快速算法
最短路徑快速算法一般情況下,對於一張隨機圖,基於實驗獲得的平均時間複雜度為 。
最壞情況下的性能
 最短路徑快速算法
最短路徑快速算法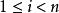 最短路徑快速算法
最短路徑快速算法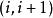 最短路徑快速算法
最短路徑快速算法 最短路徑快速算法
最短路徑快速算法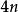 最短路徑快速算法
最短路徑快速算法下面是一種觸發該算法低性能表現的數據構造方式。假設要求從節點1到節點 的最短路徑。對於整數 ,考慮添加邊 並令其權為一個隨機的小數字(於是最短路應為1-2-...- ),同時隨機添加 條其他的權較大的邊。在這種情況下,SPFA算法的性能表現將會非常低下。
最佳化技巧
 最短路徑快速算法
最短路徑快速算法 最短路徑快速算法
最短路徑快速算法 最短路徑快速算法
最短路徑快速算法SPFA算法的性能很大程度上取決於用於鬆弛其他節點的備選節點的順序。事實上,如果 是一個優先佇列,則這個算法將極其類似於戴克斯特拉算法。然而儘管這一算法中並沒有用到優先佇列,仍有兩種可用的技巧可以用來提升佇列的質量,並且藉此能夠提高平均性能(但仍無法提高最壞情況下的性能)。兩種技巧通過重新調整 中元素的順序從而使得更靠近源點的節點能夠被更早地處理。因此一旦實現了這兩種技巧, 將不再是一個先進先出佇列,而更像一個鍊表或雙端佇列。
 最短路徑快速算法
最短路徑快速算法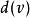 最短路徑快速算法
最短路徑快速算法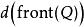 最短路徑快速算法
最短路徑快速算法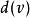 最短路徑快速算法
最短路徑快速算法 最短路徑快速算法
最短路徑快速算法距離小者優先 (Small Label First,SLF),在偽代碼的第十一行,將總是把 壓入佇列尾端修改為比較 和 ,並且在 較小時將 壓入佇列的頭端。這一技巧的偽代碼如下(這部分代碼插入在上面的偽代碼的第十一行後):
距離大者置後(Large Label Last,LLL),在偽代碼的第十一行,我們更新佇列以確保佇列頭端的節點的距離總小於平均,並且任何距離大於平均的節點都將被移到佇列尾端。偽代碼如下: