解釋
在物理學中,信號通常是波的形式,例如電磁波、隨機振動或者聲波。當波的頻譜密度乘以一個適當的係數後將得到每單位頻率波攜帶的功率,這被稱為信號的 功率譜密度(power spectral density, PSD)或者 譜功率分布(spectral power distribution, SPD)。功率譜密度的單位通常用每赫茲的瓦特數(W/Hz)表示,或者使用波長而不是頻率,即每納米的瓦特數(W/nm)來表示。
儘管並非一定要為信號或者它的變數賦予一定的物理量綱,下面的討論中假設信號在時域內變化。
定義
能量譜密度
能量譜密度描述的是信號或者時間序列的能量或者變化如何隨著頻率分布。如果 是一個有限能量信號,即平方可積,那么信號的譜密度 就是信號連續傅立葉變換幅度的平方。
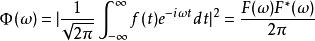 譜密度
譜密度其中 是角頻率(循環頻率的 倍), 是 的連續傅立葉變換。 是的共軛函式。
如果信號是離散的 ,經過有限的元素之後,仍然得到能量譜密度:
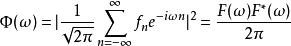 譜密度
譜密度其中 是 的離散時間傅立葉變換。如果所定義的數值個數是有限的,這個序列可以看作是周期性的,使用離散傅立葉變換得到離散頻譜,或者用零值進行擴充從而可以作為無限序列的情況計算譜密度。
乘數因子 經常不是絕對的,它隨著不同傅立葉變換定義的歸一化常數的不同而不同。
功率譜密度
上面能量譜密度的定義要求信號的傅立葉變換必須存在,也就是說信號平方可積或者平方可加。一個經常更加有用的替換表示是 功率譜密度(PSD),它定義了信號或者時間序列的功率如何隨頻率分布。這裡功率可能是實際物理上的功率,或者更經常便於表示抽象的信號被定義為信號數值的平方,也就是當信號的負載為1歐姆(ohm)時的實際功率。此瞬時功率(平均功率的中間值)可表示為:
由於平均值不為零的信號不是平方可積的,所以在這種情況下就沒有傅立葉變換。幸運的是維納-辛欽定理(Wiener-Khinchin theorem)提供了一個簡單的替換方法,如果信號可以看作是平穩隨機過程,那么功率譜密度就是信號自相關函式的傅立葉變換。
信號的功率譜密度若且唯若信號是廣義的平穩過程的時候才存在。如果信號不是平穩過程,那么自相關函式一定是兩個變數的函式,這樣就不存在功率譜密度,但是可以使用類似的技術估計時變譜密度。
屬性
· f(t)的譜密度和 f(t)的自相關組成一個傅立葉變換對(對於功率譜密度和能量譜密度來說,使用著不同的自相關函式定義)。
· 通常使用傅立葉變換技術估計譜密度,但是也可以使用如Welch法(Welch's method)和最大熵這樣的技術。
· 傅立葉分析的結果之一就是Parseval定理(Parseval's theorem),這個定理表明能量譜密度曲線下的面積等於信號幅度平方下的面積,總的能量是:
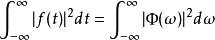 譜密度
譜密度:上面的定理在離散情況下也是成立的。另外的一個結論是功率譜密度下總的功率與對應的總的平均信號功率相等,它是逐漸趨近於零的自相關函式。
相關概念
· 大多數“頻率”圖實際上僅僅表示了譜密度。有時完整的頻率要用兩部分來表示,一部分是對應於頻率的“幅度”(它就是譜密度),另外一部分是對應於頻率的“相位”(它包含了頻譜中剩餘的其它信息)。信號 f(t) 可以從一個完整的頻譜進行恢復。需要注意的是 f(t) 不能僅僅從譜密度這一部分進行恢復——它丟失了“臨時信息”。
· 信號的 譜矩心(spectral centroid) 是譜密度函式的中點,也就是說將整個分布切分成兩個相等部分的點。
· 譜密度是頻率的函式,而不是時間的函式。但是,也可以計算一個較長信號上一小段“視窗”的譜密度,並且根據與事件相關的視窗進行繪圖,這樣的圖形稱為頻(spectrogram)。這是短時傅立葉變換和小波等許多譜分析技術的基礎。
套用
電子工程
信號功率譜的概念和套用是電子工程的基礎,尤其是在電子通信系統中,例如無線電和微波通信、雷達以及相關係統。人們已經花費了很大的精力和大量的金錢投入到開發、生產“頻譜分析儀”這種電子設備,用來幫助電子工程師、技術人員、技工觀察、測量電子信號的功率譜。頻譜分析儀的價格根據頻寬和精度的不同而不同,質量最好的儀器的價格超過 100,000 美元。
色度學
File:En:SPD.png
主條目:Colorimetry
光源的頻譜是每個頻率攜帶的功率或者光源中“顏色”的度量。光譜通常是沿著可見光在波長空間而不是頻率空間測量的不同點(通常是 31 個點)進行測量,它不是嚴格意義上的譜密度。一些分光光度計能夠分辨高達 1 到 2 納米 的增量精度,測量值用來計算其它的規格然後繪製出來顯示光源的頻譜屬性。這對於分析特定光源的顏色特性來說是一個非常有用的工具。

