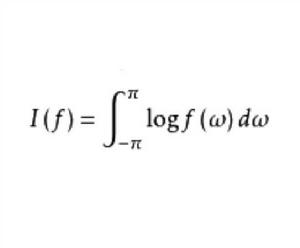基本概念
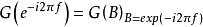 譜熵
譜熵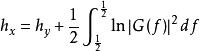 譜熵
譜熵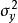 譜熵
譜熵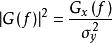 譜熵
譜熵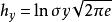 譜熵
譜熵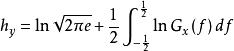 譜熵
譜熵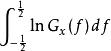 譜熵
譜熵設y是一個穩定的因果系統的輸入,該系統的傳遞函式為G (B)(它在單位園內無極點), ,x為系統的平穩輸出,則可以證明,系統的輸入與輸出的熵率之間的關係為 。這一關係在時間序列中套用最多的是輸入{y}為零的值白噪聲,方差為 ,這時系統的傳遞函式 ,而白噪聲的熵率為 ,由此得到{x}的熵率為 。以白噪聲為輸入的線性平穩系統恰是時間序列ARMA模型,上面的關係式反映了{x}的譜密度和它的熵率之間的關係。式中右邊第一項是常數,比較h的大小等價於比較第二項積分的大小,因此稱 為序列{x}的譜熵,其含意即是用功率譜來表示的熵。
熵譜與極大熵譜估計
估計平穩隨機過程功率譜密度的方法,這種方法在外推時能使自相關函式在未知點的取值具有最大統計自由度。J.P.伯格於1967年首先提出這種方法並把它稱為極大熵譜估計。極大熵譜估計最初套用於地球物理學領域地震記錄數據的分析,後來在雷達、聲納、圖像處理、語言分析以及生物醫學等領域都有廣泛的套用。
在統計學中,熵是對各種隨機試驗不確定程度的一種度量。機率分布的熵越大、試驗的可能結果越不確定。伯格的思想是要在外推相關函式的每一步,都既能保證相關函式的已知部分不變,又能在新增加外推值之後使機率分布具有最大的熵;也就是在每步外推時不對未知點處自相關函式取值施加任何限制(即其取值具有最大統計自由度,不對它強加任何條件)。極大熵譜估計的這種特點能克服傳統的功率譜估計方法解析度不高的弱點。在理論上,過程的功率譜是自相關函式的傅立葉變換。傳統的功率譜估計方法是將樣本自相關函式乘以某種窗函式(即對自相關函式加權),然後再作傅立葉變換。窗函式可以增加譜估計的穩定性並減少譜的泄漏,但窗函式會限制譜的分辨力。傳統方法存在的問題實際上是由於它把沒有觀測到的數據(或其自相關函式)都看作為零,同時對已知部分的信息加以人為修改(加權)而引起的。而極大熵譜估計對已知的最大遲延以外的自相關函式進行合理的外推,因而能提高所求功率譜的分辨力,特別是在已知數據量較少時,其效果比傳統方法更優。
極大熵譜估計是以極大熵為準則的譜估計,設f(ω)是平穩序列x(t=0,±1,…)的正規化譜(密度函式),稱
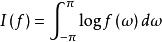 譜熵
譜熵為平穩序列x的 譜熵。假定x的前m+1個自協方差函式值
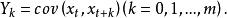 譜熵
譜熵已知,在約束
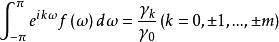 譜熵
譜熵下,使得譜熵I(f)達到極大值,以此作為準則,所得到的估計稱為 極大熵譜估計。給定觀察值x,x,…,x,利用樣本自協方差函式γ代替自協方差函式,求解上述變分問題可得到極大熵譜估計。而此問題實質上歸於求解尤爾-沃克方程
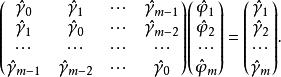 譜熵
譜熵令
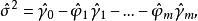 譜熵
譜熵最後得出極大熵譜估計
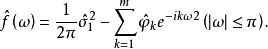 譜熵
譜熵 譜熵
譜熵所以又稱此 為譜的矩估計。