背景
隨著大量非線性負荷的投入使用，越來越多的諧波注入到電網中，使得電網諧波污染引起的電能質量問題越來越嚴重。為有效地治理諧波，必須首先確定電網諧波的分布與狀態。但在感興趣的所有節點上都安裝電能質量監測裝置是不可能的，為此，需根據有限節點上測量的各次諧波電壓和電流值，通過網路分析估算出未知節點的各次諧波電壓以及各支路的諧波電流，以掌握整個系統的諧波狀況，為諧波分析和治理提供科學的依據，這就是電力系統諧波狀態估計問題。
發展概況
早期的諧波狀態估計技術選取功率作為量測量是受到傳統電力系統狀態估計影響的結果，但因諧波無功功率的定義存在爭議且其測量裝置沒有統一的標準，由此，採用無功功率的方法依據不足。隨著基於全球定位系統（GPS）的相量測量裝置（PMU）的出現以及相應的廣域測量系統（WAMS）在電力系統的逐步建設，調度中心可以獲得一種新型的實時測量數據———相量量測，它主要包括節點電壓的幅值、相角量測和支路電流的幅值、相角量測， 有的系統還包括發電機節點的功角量測。
與SCADA系統相比，相量量測主要有以下幾個特點：增加了一種測量類型，即相角量測；數據測量精度高，這主要源於測量裝置的等級高以及數據測量同步性好，即測量同步誤差小兩方面；數據採集、傳輸速度非常快。由於技術的發展，諧波量的同步測量成為可能，為此，近年來在諧波狀態估計研究中基本採用諧波同步相量作為量測量，而不採用功率作為量測量，這樣可使得狀態估計方程線性化，計算量減小並可提高估計的精度。
目前，諧波狀態估計研究主要集中在諧波狀態估計建模、諧波狀態估計的求解算法、諧波狀態估計的可觀性和誤差、PMU 量測最佳化配置等方面。
諧波狀態估計技術
國外對於諧波狀態估計問題研究較早，1989年著名學者Heydt就提出了諧波狀態估計問題，認為諧波狀態估計是諧波潮流的逆問題，並提出了一種利用最小方差估計器的諧波源識別算法。作者利用關聯矩陣建立了諧波量測量與狀態變數之間的數學模型，選用注入視在功率和線路視在功率作量測量，並將節點分為非諧波源和可疑諧波源兩種類型，以減少未知狀態變數的數目。但是在波形畸變的情況下，無功功率的定義尚未得到統一認識，因此採用視在功率的方法欠缺說服力，但研究開創了諧波狀態估計研究的先河，具有重要的意義。
Meliopoulos 和張帆等人的研究成果中將諧波狀態估計問題看作為最佳化問題，並給出了一種最小方差估計算法。
Ma Haili和Girgis在1996年提出了一種套用卡爾曼濾波器識別諧波源的新算法，適用於非平衡三相電力系統中諧波測量儀表的最佳化配置，以及諧波源位置及其注入電流大小的最優動態估計。以諧波電流為狀態變數，諧波電壓為量測量，建立狀態方程和量測方程。對於確定數目的諧波測量儀表，通過計算不同配置條件時誤差協方差矩陣的跡，得到諧波測量儀表的最佳配置方案和諧波注入的最優估計值。
由於電網中非諧波源母線的數量可能遠大於諧波源母線數量，為減少未知狀態變數的數目，杜振平和Arrillaga提出了一種電力系統連續諧波的狀態估計算法。利用關聯矩陣的概念建立起諧波量測量與狀態變數的數學模型，並且將系統母線分為非諧波源母線和可能的諧波源母線兩種類型；此外，還將可能的諧波源母線分為測量母線和未測母線兩類。採用上述方法可極大減少未知狀態變數的數目，從而極大減少計算工作量，同時還可使諧波估計方程由欠定變為超定，增加了估計結果的可信度。
2000 年， S.S.Matair 和Watson 提出將奇異值分解（Singular Value Decomposition，簡稱SVD）算法用於電力系統諧波狀態估計，該算法能夠在系統非完全可觀即部分可觀、估計方程欠定時的情況下進行有效估計， 降低了對測量冗餘的要求。當系統完全可觀，估計方程正定或超定時，SVD 算法能給出一個唯一解，並以紐西蘭南島220 kV電網為例，分別給出系統完全可觀、部分可觀時的狀態估計結果，並且與實際值進行對比，對比結果表明奇異值分解法能夠在系統可觀、部分可觀的情況下給出有效估計值。
選擇節點電壓作為狀態量，母線注入電流、母線電壓、支路電流同步量測作為量測量進行狀態估計。對於有足夠測量（超定）的方程且測量方程無病態時，通過節點編號最佳化，運用分層算法對測量矩陣進行預處理後再進行矩陣求解；對於測量方程病態、欠定時，採用SVD算法進行求解諧波狀態估計問題，求得估計方程的最小二乘解。以IEEE14節點系統為例，建立系統模型，運用MATLAB編程仿真驗證了算法的可靠性。而且，還在SVD 算法的基礎上分析了部分可觀系統的測量問題，進而對測量配置進行了最佳化。
2004 年，吳篤貴、徐政提出了一種基於相量測量裝置PMU（Phasor Measurement Unit）的狀態估計方法。選取節點電壓相量作為狀態變數，節點電壓、支路電流和注入電流相量作為量測量，採用加權最小二乘法進行狀態估計。
上述的諧波狀態估計方法都有自己的特點，在某種特定的條件下可在一定程度上實現諧波狀態估計，但也均存在一定的缺點，精度高、速度快與可觀性好的諧波狀態估計方法的研究還需進一步深化。
諧波狀態估計數學描述
為進行諧波狀態估計，需按照一定的估計準則，對量測值進行處理，以得到目標函式的最優狀態值。雖然有很多方法均可套用於諧波狀態估計領域，如最小方差估計、極大驗後估計、極大似然估計和最小二乘估計以及由其衍生出來的加權最小二乘估計算法等，然而由於最小二乘法具有所需的先驗統計知識少、算法簡單、計算量小與收斂性好等特點，其在諧波狀態估計領域得到了更廣泛的套用。
在給定網路結線、支路參數和量測系統的條件下，諧波狀態估計的量測方程可寫為：
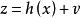諧波狀態估計 式中：
z ———量測量；
x ———狀態變數，一般是節點電壓幅值和相位；
v ———量測誤差。
對電力系統諧波狀態估計問題，引入PMU量測裝置以後，存在其節點電壓、支路電流和注入電流相量量測與狀態量節點電壓相量的線性關係，從而，諧波狀態估計數學模型大大簡化。在測量噪聲可以忽略不計的情況下，即有如下的線性狀態方程:
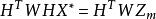諧波狀態估計 式中：
H———量測矩陣，與系統具體的拓撲結構以及量測點的配置有關；
X ———系統狀態變數；
Z———系統量測量；
W———量測加權矩陣。
求解該方程，則得到諧波狀態問題的最優估計值。
在此基礎上，對於同一個系統的狀態方程，應根據量測的不同情況採用不同的求解算法。
量測點的最佳化配置
諧波狀態估計的質量是量測數量和量測裝置安裝地點的函式。在實際電力系統中，具有諧波量測功能的裝置的配置畢竟是有限的，從經濟角度考慮不可能在感興趣的所有節點都裝設。因此，在有限數量的量測裝置情況下，為達到狀態估計的目的，需要進行量測點最優配置問題的研究，以得到最優量測裝置數量及量測點位置。
Heydt 首次提出採用係數矩陣的最小條件數法進行諧波量測點配置。針對靜態諧波狀態估計提出了一種混合非線性最小二乘法，然而，它研究的是選擇一個最優位置放置一個量測裝置來確定諧波源的問題，而不是選擇量測裝置的最優數量和對諧波數量的準確估計的評價。
通過算例分析比較了粒子群算法與遺傳算法、枚舉法在量測配置方案的計算收斂速度，對安裝不同數量量測設備的配置問題，套用粒子群算法能夠得到最優解，並且收斂速度相對較快。
研究展望
a）進行諧波狀態估計中發電機、變壓器、輸電線路以及諧波源等模型建立方面的進一步研究。
b）對諧波狀態估計算法進一步研究，可以借鑑現有電力系統基波狀態估計方法，提出更具普遍和實用性的新算法。
c）對量測點的最佳化配置原則進一步研究，在保證系統可觀性的條件下合理布局量測設備的安置地點，以更經濟的方式使狀態估計的結果質量更高。
d）研究與開發具有同步時標的電能質量監測設備，綜合監控電能質量各個指標，降低PMU的投資成本。
e）開展諧波狀態估計的套用研究，在套用過程中不斷提高諧波狀態估計的精度，使該項研究儘早實用化。
