誤差函式

在數學中，誤差函式（也稱之為高斯誤差函式，error function or Gauss error function）是一個非基本函式（即不是初等函式），其在機率論、統計學以及偏微分方程中都有廣泛的套用。在統計學與機率論中，高斯函式是常態分布的密度函式，根據中心極限定理它是複雜總和的有限機率分布。高斯函式是量子諧振子基態的波函式。在數學領域，高斯函式在厄爾米特多項式的定義中起著重要作用。在光學以及微波系統中有高斯波束的套用。高斯函式在圖像處理中用作預平滑核。

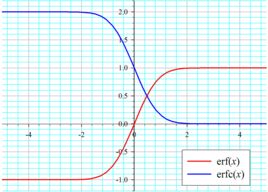
具體內容

定義

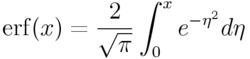誤差函式

且有erf(∞)=1和erf(-x)=-erf(x)。

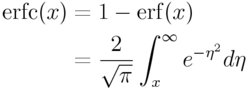誤差函式

導數與積分

誤差函式的導數為：

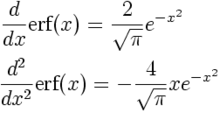誤差函式

等等

誤差函式的重積分定義為：

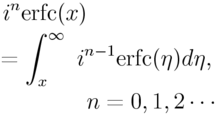誤差函式

且

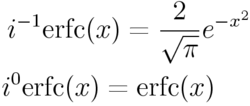誤差函式

可得

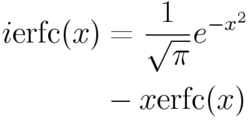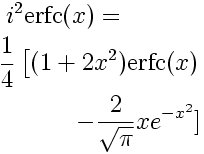誤差函式

誤差函式

級數展開式

誤差函式的級數展開式為：

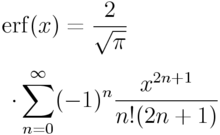誤差函式

套用

高斯函式的不定積分是誤差函式。在自然科學、社會科學、數學以及工程學等領域都有高斯函式的身影，這方面的例子包括：

在統計學與機率論中，高斯函式是常態分布的密度函式，根據中心極限定理它是複雜總和的有限機率分布。

高斯函式是量子諧振子基態的波函式。

計算化學中所用的分子軌道是名為高斯軌道的高斯函式的線性組合（參見量子化學中的基組）。

在數學領域，高斯函式在厄爾米特多項式的定義中起著重要作用。

高斯函式與量子場論中的真空態相關。

在光學以及微波系統中有高斯波束的套用。

高斯函式在圖像處理中用作預平滑核。