造成中誤差的原因
 中誤差
中誤差由某種固定的原因造成的,使測定結果偏高或偏低,重複測定時會重複出現,系統誤差的大小几乎是一個恆定值,因而又被稱之為恆定誤差或可測誤差。它產生的原因有以下幾點:
系統誤差
由某種固定的原因造成的,使測定結果偏高或偏低,重複測定時會重複出現,系統誤差的大小几乎是一個恆定值,因而又被稱之為恆定誤差或可測誤差。它產生的原因有以下幾點:
儀器誤差:儀器本身不夠精度或未經校正所引起的,如天平、砝碼和量器刻度不夠準確。為避免引起儀器誤差,我們應對所使用的量器及天平進行校正。
試劑誤差:由於試劑不純或蒸餾水中含有微量雜質所引起的誤差。消除方法可進行空白實驗,在不加試樣的情況下,按照被測試樣的分析步驟和條件進行分析,得到的結果為空白值,從試樣的分析結果中減去“空白值”就可以得到更接近真實含量的分析結果。
方法誤差:這種誤差是由於分析方法本身所造成的。如重量分析時,由於沉澱的溶解造成損失或因吸附某些雜質而產生誤差;或滴定分析中,因為反應不完全或干擾離子的影響,以及滴定終點和等當點不符合等。
操作誤差:正常操作條件下,由於分析人員掌握操作規程與正確控制條件捎有出入而引起的誤差。如滴定管讀數時偏高或偏低,對某種顏色的變化辨別不夠敏銳等所造成的誤差。
偶然誤差
偶然誤差也稱不定誤差,它是由某些偶然因素:測定時環境的溫度、濕度氣壓的微小波動,或由於外界條件的影響而使安放在操作台上的天平受到微小的震動所引起的。其影響有時大、有時小。因而偶然誤差難以察覺,也難以控制。
隨著測定次數的增加偶然誤差的算術平均值將逐漸接近於零。因而有必要時,應多次測定 ,但並非實驗次數越多越好,這樣只浪費更多的人力、物力。一般測定中,做2~3次平行測定可達到不超過規定誤差的目的。
粗差
粗差即粗大誤差,是指比在正常觀測條件下所可能出現的最大誤差還要大的誤差,通俗地說,粗差要比偶然誤差大上好幾倍。例如觀測時大數讀錯,計算機輸入數據錯誤,航測像片判讀錯誤,控制網起始數據錯誤等。這種錯誤或誤差,在一定程度上可以避免。但在使用現今的高新測量技術如全球定位系統(GPS)、地理信息系統(GIS)、遙感(RS)以及其他高精度的自動化數據採集中,經常是粗差混入信息之中,識別粗差源並不是簡單方法可以達到目的的,需要通過數據處理方法進行識別和消除其影響。
計算公式
測量誤差按其對測量結果影響的性質,可分為:
一.系統誤差(system error)
1.定義:在相同觀測條件下,對某量進行一系列觀測,如誤差出現符號和大小均相同或按一定的規律變化,這種誤差稱為系統誤差。
2.特點:具有積累性,對測量結果的影響大,但可通過一般的改正或用一定的觀測方法加以消除。
二.偶然誤差(accident error)
1.定義:在相同觀測條件下,對某量進行一系列觀測,如誤差出現符號和大小均不一定,這種誤差稱為偶然誤差。但具有一定的統計規律。
2.特點:
(1)具有一定的範圍。
(2)絕對值小的誤差出現機率大。
(3)絕對值相等的正、負誤差出現的機率相同。
(4)數學期限望等於零。即:
誤差機率分布曲線呈常態分配,偶然誤差要通過的一定的數學方法(測量平差)來處理。
此外,在測量工作中還要注意避免粗差(gross error)(即:錯誤)的出現。
§2衡量精度的指標
測量上常見的精度指標有:中誤差、相對誤差、極限誤差。
一.中誤差
方差
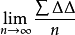 中誤差
中誤差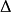 中誤差
中誤差——某量的真誤差,∑——求和符號。
規律:標準差估值(中誤差m)絕對值愈小,觀測精度愈高。
在測量中,n為有限值,計算中誤差m的方法,有:
1.用真誤差(true error)來確定中誤差——適用於觀測量真值已知時。
真誤差Δ——觀測值與其真值之差,有:
標準差
中誤差(標準差估值), n為觀測值個數。
2.用改正數來確定中誤差(白塞爾公式)——適用於觀測量真值未知時。
V——最或是值與觀測值之差。一般為算術平均值與觀測值之差,即有:
二.相對誤差
1.相對中誤差
2.往返測較差率K
三.極限誤差(容許誤差)
常以兩倍或三倍中誤差作為偶然誤差的容許值。即:。
§3誤差傳播定律
一.誤差傳播定律
設、…為相互獨立的直接觀測量,有函式
,則有:
二.權(weight)的概念
1.定義:設非等精度觀測值的中誤差分別為m1、m2、…mn,則有:
權其中,n為任意大小的常數。
當權等於1時,稱為單位權,其對應的中誤差稱為單位權中誤差(unit weight mean squareerror)m0,故有:。
2.規律:權與中誤差的平方成反比,故觀測值精度愈高,其權愈大。