基本概述
【英文】：
an error; inaccuracy;deviation
【中文拼音】：
wù chā
【基本解釋】：
一個量的觀測值或計算值與其真實值之差;特指統計誤差，即一個量在測量、計算或觀察過程中由於某些錯誤或通常由於某些不可控制的因素的影響而造成的變化偏離標準值或規定值的數量 ，誤差是不可避免的。
【詳細解釋】：
1.猶差錯。 漢荀悅《漢紀·文帝紀下》：“上功莫府，差六級，文吏以法繩之，陛下下之吏，削其爵，罰作之。” 唐趙璘《因話錄·徵》：“談話之誤差尚可，若著於文字，其誤甚矣。”
2.數學上稱測定的數值或其他近似值與真值的差為誤差。
準確度與誤差
真值是試樣中待測組分客觀存在的真實含量。準確度是分析結果與真值的相符程度。準確度通常用誤差來表示，誤差越小，表示分析結果的準確度越高 。
誤差可以用絕對誤差和相對誤差來表示。絕對誤差是分析結果與真值之差，表示為：
E=x-T
x代表單次測定值。由於測定次數往往不止一次，因此通常用數次平行測定結果的算術平均值來表示分析結果。此時：
E=x-T
相對誤差是絕對誤差和真值的百分比率：
E=E/T´ 100%
當測定值大於真值時，誤差為正，表明測定結果偏高；反之，誤差為負，表明測定值偏低。在測定的絕對誤差相同的條件下，待測組分含量越高，相對誤差越小；反之，相對誤差越大。因此，在實際工作中，常用相對誤差表示測定結果的準確度。
有時也採用中位數來表示分析結果。中位數即一組測定數據從小至大進行排列時，處於中間的那個數據或中間相鄰兩個數據的平均值。用中位數表示分析結果比較簡單，但存在不能充分利用數據的缺點。
由於誤差不可避免地存在於測定中，所以任何真值都難以得知。在實際工作中，通常將純物質中元素的理論含量等理論真值，國際計量大會上確定的長度、質量和物質的量單位等計量數約定真值，或公認的機構發售的標準參考物質（也成為標準試樣）給出的參考值等當作真值來使用。
例題：用沉澱滴定法測定純Nacl中氯的質量分數為60.56%、60.46%、60.70%、60.65%、60.90%。試計算測定結果的絕對誤差和相對誤差。
解：純Nacl中氯的質量分數的理論值（真值）為T：
T=M/MX100%=35.45/58.44X100%=60.66%
平均值：x=(60.56%+60.46%+60.70+60.56+60.69%)/5=60.61%
絕對誤差：E=x-T=60.61%-60.66%=-0.05%
相對誤差：E=E/TX100%=(-0.05%)/60.66%=-0.09%
定義
一個量的觀測值或計算值與其真實值之差，特指統計誤差，即一個量在測量、計算或觀察過程中由於某些錯誤或通常由於某些不可控制的因素的影響而造成的變化偏離標準值或規定值的數量 。
數學上稱測定的數值或其他近似值與真值的差為誤差。
誤差 設被測量的真值（真正的大小）為a，測得值為x，誤差為ε，則：
x-a=ε
誤差與錯誤不同，錯誤是應該而且可以避免的，而誤差是不可能絕對避免的。從實驗的原理，實驗所用的儀器及儀器的調整，到對物理量的每次測量，都不可避免地存在誤差，並貫穿於整個實驗始終。
測量值與真值之差異稱為誤差。
測量時，由於各種因素會造成少許的誤差，這些因素必須去了解，並有效的解決，方可使整個測量過程中誤差減至最少。測量時，造成誤差的主要有系統誤差和隨機誤差，而系統誤差有下列情況：視差、刻度誤差、磨耗誤差、接觸力誤差、撓曲誤差、餘弦誤差、阿貝(Abbe) 誤差、熱變形誤差等。系統誤差的大小在測量過程中是不變的，可以用計算或實驗方法求得，即是可以預測，並且可以修正或調整使其減少。這些因素歸納成五大類，詳細內容敘述如下。
產生
根據誤差產生的原因及性質可分為系統誤差與偶然誤差兩類。
系統誤差
系統誤差又稱可測誤差，它是由分析操作過程中的某些經常發生的原因造成的。
主要來源有以下幾個方面：
①儀器誤差：是由使用的儀器本身不夠精密所造成的
②方法誤差：是有分析方法本身造成的
③試劑誤差：是由所用蒸餾水含有雜質或使用的試劑不純造成的
④操作誤差：是由操作人員掌握分析操作的條件不成熟、個人觀察器官不敏銳和固有的習慣造成的
⑤主觀誤差：是由操作人員主觀原因，如觀察判斷能力的缺陷或不良習慣造成的
偶然誤差
在相同條件下，對同一物理量進行多次測量，由於各種偶然因素，會出現測量值時而偏大，時而偏小的誤差現象，這種類型的誤差叫做偶然誤差。
產生偶然誤差的原因很多，例如讀數時，視線的位置不正確，測量點的位置不準確，實驗儀器由於環境溫度、濕度、電源電壓不穩定、振動等因素的影響而產生微小變化等等。這些因素的影響一般是微小的，而且難以確定某個因素產生的具體影響的大小，因此偶然誤差難以找出原因加以排除。
但是實驗表明，大量次數的測量所得到的一系列數據的偶然誤差都服從一定的統計規律，這些規律有：
（1）絕對值相等的正的與負的誤差出現機會相同；
（2）絕對值小的誤差比絕對值大的誤差出現的機會多；
（3）誤差不會超出一定的範圍。
實驗結果還表明，在確定的測量條件下，對同一物理量進行多次測量，並且用它的算術平均值作為該物理量的測量結果，能夠比較好地減少偶然誤差。
表示
絕對誤差
設某物理量的測量值為x,它的真值為a，則x－a=ε；由此式所表示的誤差ε和測量值x具有相同的單位，它反映測量值偏離真值的大小，所以稱為絕對誤差（即測量值與真實值之差的絕對值）。
絕對誤差可定義為：
△=X-L
式中：△—絕對誤差 X—測量值 L—真實值
註：絕對誤差有正負性，正性表示測量值大於真實值，負性表示測量值小於真實值。
相對誤差
誤差還有一種表示方法，叫相對誤差，它是絕對誤差與測量值或多次測量的平均值的比值，即或，並且通常將其結果表示成非分數的形式，所以也叫百分誤差。
絕對誤差可以表示一個測量結果的可靠程度，而相對誤差則可以比較不同測量結果的可靠性。
例如，測量兩條線段的長度，第一條線段用最小刻度為毫米的刻度尺測量時讀數為10.3毫米，絕對誤差為0.1毫米（值讀得比較準確時），相對誤差為0.97%，而用準確度為0.02毫米的遊標卡尺測得的結果為10.28毫米，絕對誤差為0.02毫米，相對誤差為0.19%；第二條線用上述測量工具分別測出的結果為19.6毫米和19.64毫米，前者的絕對誤差仍為0.1毫米，相對誤差為0.51%，後者的絕對誤差為0.02毫米，相對誤差為0.1%。比較這兩條線的測量結果，可以看到，用相同的測量工具測量時，絕對誤差沒有變化，用不同的測量工具測量時，相對誤差明顯不同，準確度高的工具所得到的相對誤差小。然而相對誤差則不僅與所用測量工具有關，而且也與被測量的大小有關，當用同一種工具測量時，被測量的數值越大，測量結果的相對誤差就越小。
引用誤差
儀表某一刻度點讀數的絕對誤差Δ比上儀表量程上限Am ，並用百分數表示。
最大引用誤差：儀表在整個量程範圍內的最大示值的絕對誤差Δm比儀表量程上限Am ，並用百分數表示。
標稱誤差
標稱誤差=（最大的絕對誤差）/量程 x 100%。
測量儀器的示值誤差是指“測量儀器示值與對應輸入量的真值之差”(7.20條)。這是測量儀器的最主要的計量特性之一，其實質就是反映了測量儀器準確度的大小。示值誤差大則其準確度低，示值誤差小，則其準確度高。
示值誤差是對真值而言的。由於真值是不能確定的，實際上使用的是約定真值或實際值。為確定測量儀器的示值誤差，當其接受高等級的測量標準器檢定或校準時，則標準器復現的量值即為約定真值，通常稱為實際值，即滿足規定準確度的用來代替真值使用的量值。所以指示式測量儀器的示值誤差=示值-實際值；實物量具的示值誤差=標稱值-實際值。
例如：被檢電流表的示值I為40A，用標準電流表檢定，其電流實際值為I=41A，則示值40A的誤差Δ為
Δ=I-I=40-41=-1A
則該電流表的示值比其真值小1A。如一工作玻璃量器的容量其標稱值V為1000ml，經標準玻璃量器檢定，其容量實際值V為1005ml，則量器的示值誤差Δ為：
Δ=V-V=1000-1005=-5ml
即該工作量器的標稱值比其真值小5ml。
要正確區別誤差、偏差和修正值的概念。偏差是指“一個值減去其參考值”(5.17條)，對於實物量具而言，偏差就是實物量具的實際值對於標稱值偏離的程度，即偏差=實際值-標稱值。例如有一塊量塊，其標稱值為10mm，經檢定其實際值為10.1mm，則該量塊的偏差為10.1-10=+0.1mm，說明此量塊相對10mm標準尺寸大了0.1mm；則此量塊的誤差為示值(標稱值)-實際值，即誤差=10-10.1=-0.1mm，說明此量塊比真值小了0.1mm，故此在使用時應加上0.1mm修正值。修正值是指為清除或減少系統誤差，用代數法加到未修正測量結果上的值。從上可見這三個概念其量值的關係：誤差=-偏差；誤差=-修正值；修正值=偏差。在日常計算和使用時要注意誤差和偏差的區別，不要相混淆。
基值誤差
它是指“為核查儀器而選用在規定的示值或規定的被測量值處的測量儀器誤差”(7.22條)。為了檢定或校準測量儀器，人們通常選取某些規定的示值或規定的被測量值，則在該值上測量儀器的誤差稱為基值誤差。
例如:選用規定的示值，如對普通準確度等級的衡器，載荷點50e和200e是必檢的(e是衡器的檢定分度值)，它們在首次檢定時基值誤差分別不得超過±0.5e和±1.0e。
如對於中準確度等級的衡器，載荷點500e和2000e是必須檢的，它們在首次時的基值誤差分別不得超過±0.5e和±1.0e。規定被測量值，如對於標準熱電偶的檢定或分度，通常選用鋅、銻及銅三個溫度固定點進行示值檢定或分度，則在此三個值上標準熱電偶的誤差，即為基值誤差。測量儀器的基值誤差可簡稱為基值誤差。
零值誤差
它是指“被測量為零值的基值誤差”(7.23條)。是指被測量為零值時，測量儀器示值相對於標尺零刻線之差值。也可說是測量儀器零位，即當被測量值為零時，測量儀器的直接示值與標尺零刻線之差。通常在測量儀器通電情況下，稱為電氣零位，在不通電的情況下稱為機械零位。零位在測量儀器檢定或校準或使用時十分重要，因為它無需用標準器就能準確地確定其零位值，如各種指示儀表和千分尺、度盤秤等都具有零位調節器，可以作為檢定或校準或用作使用者調整，以便確保測量儀器的準確度。
通常測量儀器零值誤差均作為基值誤差對待，因為零值對考核測量儀器的穩定性、準確度作用十分重要。測量儀器的零值誤差可簡稱為零值誤差。
固有誤差
它是指“在參考條件下確定的測量儀器的誤差”(7.24條)。固有誤差通常也可稱為基本誤差，它是指測量儀器在參考條件下所確定的測量儀器本身所具有的誤差。主要來源於測量儀器自身的缺陷，如儀器的結構、原理、使用、安裝、測量方法及其測量標準傳遞等造成的誤差。固有誤差的大小直接反映了該測量儀器的準確度。一般固有誤差都是對示值誤差而言，因此固有誤差是測量儀器劃分準確度的重要依據。測量儀器的最大允許誤差就是測量儀器在參考條件下，反映測量儀器自身存在的所允許的固有誤差極限值。
提出固有誤差這一術語是相對於附加誤差而言的。附加誤差就是測量儀器在非標準條件下所增加的誤差。額定操作條件、極限條件等都屬於非標準條件。非標準(即參考)條件下工作的測量儀器的誤差，必然會比參考條件下的固有誤差要大一些，這個增加的部分就是附加誤差。它主要是由於影響量超出參考條件規定的範圍，對測量儀器帶來影響的所增加的誤差，即屬於外界因素所造成的誤差。因此測量儀器使用時與檢定、校準時因環境條件不同而引起的誤差，就是附加誤差；測量儀器在靜態條件下檢定、校準，而在實際動態條件下使用，則也會帶來附加誤差。測量儀器的固有誤差又可簡稱為固有誤差。
相關因素
人為因素
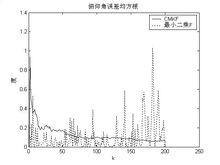最小二乘俯仰角估計誤差比較 由於人為因素所造成的誤差，包括誤讀、誤算和視差等。 而誤讀常發生在游標尺、分厘卡等量具。游標尺刻度易造成誤讀一個最小讀數，如在10.00 mm處常誤讀成10.02 mm或9.98 mm。分厘卡刻度易造成誤讀一個螺距的大小，如在10.20 mm常誤讀成10.70 mm或9.70 mm。誤算常在計算錯誤或輸入錯誤數據時所發生。視差常在讀取測量值的方向不同或刻度面不在同一平面時所發生，兩刻度面相差約在0.3~0.4 mm之間，若讀取尺寸在非垂直於刻度面時，即會產生 的誤差量。為了消除此誤差，製造量具的廠商將游尺的刻劃設計成與本尺的刻劃等高或接近等高，(游尺刻劃有圓弧形形成與本尺刻劃幾近等高，游尺為凹V形且本尺為凸V形，因此形成兩刻劃等高。
量具因素
理想和帶增益誤差的3位ADC轉換器的傳遞 由於量具因素所造成的誤差，包括刻度誤差、磨耗誤差及使用前未經校正等因素。 刻度分劃是否準確，必須經由較精密的儀器來校正與追溯。量具使用一段時間後會產生相當程度磨耗，因此必須經校正或送修方能再使用。
力量因素
由於測量時所使用接觸力或接觸所造成撓曲的誤差。 依據胡克定律，測量尺寸時，如果以一定測量力使測軸與機件接觸，則測軸與機件皆會局部或全面產生彈性變形，為防止此種彈性變形，測軸與機件應采相同材料製成。其次，依據赫茲(Hertz) 定律，若測軸與機件均採用鋼時，其彈性變形所引起的誤差量。
測量因素
測量時，因儀器設計或擺置不良等所造成的誤差，包括餘弦誤差、阿貝誤差等。餘弦誤差是發生在測量軸與待測表面成一定傾斜角度 。通常，餘弦誤差會發生在兩個測量方向，必須特別小心。
例如測量內孔時，徑向測量尺寸需取最大尺寸，軸向測量需取最小尺寸。同理，測量外側時，也需注意取其正確位置。測砧與待測工件表面必須小心選用，如待測工件表面為平面時需選用球狀之測砧、工件為圓柱或圓球形時應選平面之測砧。
環境因素
測量時受環境或場地之不同，可能造成的誤差有熱變形誤差和隨機誤差為最顯著。 熱變形誤差通常發生於因室溫、人體接觸及加工後工件溫度等情形下，因此必須在溫濕度控制下，不可用手接觸工件及量具、工件加工後待冷卻後才測量。但為了縮短加工時在加工中需實時測量，因此必須考慮各種材料之熱脹係數 作為補償，以因應溫度材料的熱膨脹係數不同所造成的誤差。
使用
最大允許誤差
是指“對給定的測量儀器，規範、規程等所允許的誤差極限值”(7.21條)。 這是指在規定的參考條件下，測量儀器在技術標準、計量檢定規程等技術規範上所規定的允許誤差的極限值。這裡規定的是誤差極限值，所以實際上就是測量儀器各計量性能所要求的最大允許誤差值。可簡稱為最大允許誤差，也可稱為測量儀器的允許誤差限。最大允許誤差可用絕對誤差、相對誤差或引用誤差等來表述。
例如：測量範圍為0～25mm，分度值為0.01mm的千分尺其示值的最大允許誤差0級不得超過±2mm；1級不得超過±4mm。又如測量範圍為25℃～50℃的分度值為0.05℃的一等標準水銀溫度計，其示值的最大允許誤差為±0.10℃。如準確度等級為1.0級的配熱電阻測溫用動圈式測量儀表，其測量範圍為0～500℃，則其示值的最大允許誤差為500×1%=±5℃，則用引用誤差表述。如非連續累計自動衡器(料斗秤)在物料試驗中，對自動稱量誤差的評定則以累計載荷質量的百分比相對誤差進行計算，準確度為0.2級、0.5級的則首次檢定其自動稱量誤差不得超過累計載荷質量的±0.10%和±0.25%。最大允許誤差是評定測量儀器是否合格的最主要指標之一，當然它也直接反映了測量儀器的準確度。
要區別和理解測量儀器的示值誤差、測量儀器的最大允許誤差和測量不確定度之間的關係。示值誤差和最大允許誤差均是對測量儀器本身而言，最大允許誤差是指技術規範(如標準、檢定規程)所規定的允許的誤差極限值，是判定是否合格的一個規定要求，而示值誤差是測量儀器某一示值其誤差的實際大小，是通過檢定、校準所得到的一個值，可以評價是否滿足最大允許誤差的要求，從而判斷該測量儀器是否合格，或根據實際需要提供修正值，以提高測量儀器的準確度。測量不確定度是表征測量結果分散性的一個參數，它只能表述一個區間或一個範圍，說明被測量真值以一定機率落於其中，它對測量結果而言，以判定測量結果的可靠性。可見最大允許誤差、示值誤差和測量不確定度它們具有不同的概念，前者相對測量儀器而言，後者相對測量結果而言，前者相對與真值(約定真值)之差，後者只是一個區間範圍，前者可以對測量儀器的示值進行修正，後者無法對測量儀器進行修正。個人認為，可見測量不確定度概念不能完全代替測量儀器的誤差，因為它無法得到修正值，作為測量儀器的特性，規定最大允許誤差和通過檢定、校準去確定示值誤差，在實用上具有十分現實的意義。
引用誤差
測量儀器的引用誤差可簡稱為引用誤差。 它是指“測量儀器的誤差除以儀器的特定值”(7.28條)。通常很多測量儀器是用引用誤差來表示該測量儀器的允許誤差限。特定值一般稱為套用值，它可以是測量儀器的量程也可以是標稱範圍的上限或測量範圍等。測量儀器的引用誤差就是測量儀器的相對誤差與其套用值之比。
真值
實際上，真值是難於得到的，實際中，人們通常用兩種方法來近似確定真值，並稱之為約定真值。
一種方法是採用相應的高一級精度的計量器具所復現的被測量值來代表真值，
另一種方法是在相同條件下多次重複測量的算術平均值來代表真值。
另外在產品檢測中，某項被測量的設計指標，既標稱值視作已知真值，而測量值與標稱值之差，就是產品製作誤差（注意：這裡的測量值與其算術平均值之差才是測量誤差）。
理論值作為真值，如三角形內角和為180°。
誤差分類
在數值計算中，為解決求方程近似值的問題，通常對實際問題中遇到的誤差進行下列幾類的區分：
模型誤差
在建立數學模型過程中，要將複雜的現象抽象歸結為數學模型，往往要忽略一些次要因素的影響，對問題作一些簡化。因此數學模型和實際問題有一定的誤差，這種誤差稱為模型誤差。
測量誤差
在建模和具體運算過程中所用的數據往往是通過觀察和測量得到的，由於精度的限制，這些數據一般是近似的，即有誤差，這種誤差稱為測量誤差。
截斷誤差
由於實際運算只能完成有限項或有限步運算，因此要將有些需用極限或無窮過程進行的運算有限化，對無窮過程進行截斷，這樣產生的誤差成為截斷誤差。
捨入誤差
在數值計算過程中，由於計算工具的限制，我們往往對一些數進行四捨五入，只保留前幾位數作為該數的近似值，這種由捨入產生的誤差成為捨入誤差。
抽樣誤差
抽樣誤差：是指樣本指標和總體指標之間數量上的差別，例如抽樣平均數與總體平均數之差 、抽樣成數與總體成數之差（p-P）等。抽樣調查中的誤差有兩個來源，分別為：
（1）登記性誤差，即在調查過程中，由於主客觀原因而引起的誤差。
（2）代表性誤差，即樣本各單位的結構情況不足以代表總體特徵而引起的誤差。
化學中的誤差
可疑測定值
在一組平行測定數據中，常會出現與其他結果相差較大的個別測定值，該值稱為可疑值或異常值（也叫離散值或者極端值等）。對於位數不多的測定數據，可疑值的取捨往往對平均值和精密度造成相當顯著的影響。
如果已經測定中發生過失，則無論此數據是否異常，一概都應捨去；而在原因不明的情況下，就必須按照一定的統計學方法進行檢驗，然後再對取捨做出判斷。以下介紹使用簡單的Q檢驗法和效果好的格魯布斯法。
Q檢驗法
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Q0.90 | 0.94 | 0.76 | 0.64 | 0.56 | 0.51 | 0.47 | 0.44 | 0.41 |
| Q0.95 | 0.97 | 0.85 | 0.73 | 0.64 | 0.59 | 0.54 | 0.51 | 0.48 |
| Q0.99 | 0.99 | 0.93 | 0.82 | 0.74 | 0.68 | 0.63 | 0.60 | 0.57 |
該法有迪安和狄克遜在1951年提出。具體步驟：
1、將一組數據有小至大按順序排列為x,x,x…x,x，假設x和或x為可疑值。
2、計算可疑值與最鄰近數據的差值，除以極差，所得的商稱為Q值。
若x為可疑值，則：
Q=(x-x)/(x-x)
若x為可疑值，則：
Q=(x-x-1)/(x-x)
例題：
用冷原子螢光法測定水中汞的含量，3次測定的結果分別為：0.001mg/L、0.002mg/L、0.009mg/L。問置信度為90%時，可疑數據“0.009”是否應捨去？
解：
Q=（0.009-0.002）/(0.009-0.001)=0.88
置信度為90%，n=3時，查表得：Q=0.94
因為：Q
若將”0.009“保留，取三次測定數據的平均值，分析結果不合理，若再測定一次數據得0.002mg/L，
此時，Q表=0.76，Q>Q表,故可以捨去可疑值0.009。
格魯布斯法
| 測定次數n | 置信度P | 測定次數n | 置信度P | ||
| 95% | 99% | 置信度P95% | 99% | ||
| 3 | 1.15 | 1.15 | 12 | 2.29 | 2.55 |
| 4 | 1.46 | 1.49 | 13 | 2.33 | 2.61 |
| 5 | 1.67 | 1.75 | 14 | 2.37 | 2.66 |
| 6 | 1.82 | 1.94 | 15 | 2.41 | 2.71 |
| 7 | 1.94 | 2.10 | 16 | 2.44 | 2.75 |
| 8 | 2.03 | 2.22 | 17 | 2.47 | 2.79 |
| 9 | 2.11 | 2.32 | 18 | 2.50 | 2.82 |
| 10 | 2.18 | 2.41 | 19 | 2.53 | 2.85 |
| 11 | 2.23 | 2.48 | 20 | 2..56 | 2.88 |
首先計算出改組數據的平均值x和標準偏差s，再計算統計量G。
根據事先確定的置信度和測定次數查閱表中G值表，如果G>G表，說明可疑值相對於平均值偏離較大，應以一定的置信度將其捨去，否則應予以保留。
在運用格魯布斯法判斷可疑值的取捨時，由於引入了t分布中最基本的兩個參數平均值和方差，故該方法的準確度較Q檢驗法高。
