定義
 規模收益遞增
規模收益遞增規模收益遞增(increasing returns to scale)
 規模收益遞增
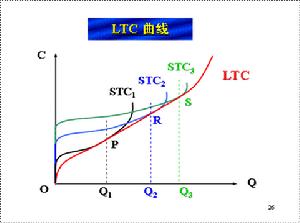
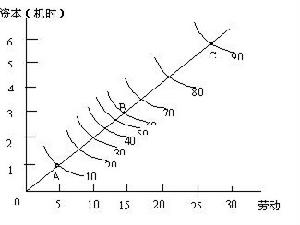
規模收益遞增生產長期分析包含的一個重要問題是考慮所有投入都變化時的產出變化情況。經濟學家利用規模收益(又稱規模報酬:Returns to scale)概念來分析所有投入品都成比例變化時產出變化情況。依據所有投入同比例變化時產出變化水平不同,存在三種規模收益情況。
在技術水平不變的條件下,所有生產要素投入量按照相同比例增加時,總產量先是以遞增的幅度增加,其次以不變的幅度增加,最後以遞減的幅度增加。相應地分別稱為規模收益遞增階段、規模收益不變階段和規模收益遞減階段。
一、規模收益遞增
二、規模收益不變
原因
增加生產規模,會使規模收益遞增。這是因為有以下因素在起作用。
(1)工人可以專業化。在小企業中,一個工人可能要做好幾種作業;在大企業中工人多,就可以分工分得更細,實行專業化。這樣就有利於工人提高技術熟練程度,有利於提高勞動生產率。
(2)可以使用專門化的設備和較先進的技術。小企業因為產量少,只能採用通用設備。大企業實行大量生產,有利於採用專用設備和較先進的技術。
(3)大設備單位能力的製造和運轉費用通常比小設備要低。例如,大高爐比小高爐、大型電機比小型電機單位能力的製造成本和運轉成本要低。
(4)生產要素具有不可分割性。例如,一座 1000噸的高爐,由於不可分割,除非產量達到1000噸,否則就不能充分利用。
(5)其他因素。如大規模生產便於實行聯合化和多種經營;便於實行大量銷售和大量採購(可以節省購、銷費用)
理論模型
遵循Ethier(1982)的基本建模思路,本文假設一個由本國和外國構成的經濟世界,有兩種生產要素:資本(K)和勞動(L)。存在兩個生產最終消費品的行業:農產品A和製成品M。農業是在完全競爭市場上利用資本和勞動生產具有規模收益不變性質的行業,其產品具有相似性;製造業由兩個二級代碼行業構成:生產最終消費品M的行業和生產中間投入品X的行業。M行業是具有投入多樣化傾向的規模收益遞增行業,其產品也具有相似性,且製造品M是利用具有差異性的中間投入品X無成本的組裝起來。因此,在無成本貿易的假設下,製造品M的市場結構是完全競爭的。
①中間投入品X行業是由生產差異產品的無數壟斷競爭廠商構成。
假設兩國間貿易不存在關稅和運輸成本等貿易障礙;兩國消費偏好和生產技術相似;國際貿易是平衡的;兩國要素均充分利用,勞動和資本要素在國內行業間可以流動,不可以跨國流動。
② 根據上述經濟運行背景假設可以看出,與要素稟賦理論相比,其主要差異在於M行業是規模收益遞增行業,且增加了一個生產差異產品的中間投入品X行業。由於X行業的生產技術具有無限的規模經濟性,Ethier(1982)稱之為“國內規模收益遞增”;而M行業在生產上具有專業性多樣化投入產生的規模收益遞增特徵,且隨著經濟自由化的發展,專業性投入品的品種將增加,被稱為“國際規模收益遞增”。從而,可以以比較靜態方式來闡述規模回報遞增與傳統貿易理論之間的理論關係。
1.消費者行為。假設兩國消費偏好具有相似性,其典型消費者擁有科布-道格拉斯效用函式,並且對製成品的支出份額為常數γ(Ethier,1982)。效用函式和預算約束方程為:
2.生產者行為。依據基本假設,農產品是利用勞動和資本生產的,且農業具有規模收益不變的特徵,因此,假定農產品的生產函式為科布-道格拉斯型的,即:
其中,假設F=r/W代表租金-工資比,即要素的相對價格。參數包。
製成品M是通過投入各種元件X無成本組裝出來,但是隨著可投入的元件種類的增加,也就是隨著勞動分工的深化,專業化的投入品使得M行業的生產率呈現規模收益遞增的性質,其生產函式為:
其中,x[,i]代表第i種元件的投入數量,n代表元件的種類數,參數α>1代表製造業的生產隨著勞動分工的深化,投入品種類的增加而表現出規模收益遞增性。參數0<β<1代表對各種元件的投入偏好,β越大,偏好越強,可替代性越差;反之亦真。投入元件之間的替代彈性σ=1/(1-β)(Dixit and Stiglitz, 1977;Krugman,1979),且σ>1;σ越大,元件之間的替代性越強;反之亦真。可以看出,隨著各種元件的投入數量等比增加,製造品生產呈現規模收益不變的性質;當元件數量增加,M行業呈現規模收益遞增現象。因此,這種行業水平上的規模收益遞增性質被Ethier(1982)稱為“國際規模收益遞增”。
中間投入品X元件也是利用資本和勞動生產出來的,其投入是在相應的要素價格下的最優要素組合構成的要素束(m),並且最優要素組合獨立於元件的最優生產規模(Either,1982)。③假設當某種元件的產出規模x,需投入要素束m的數量為(ax+b),其中a、b是大於0的參數,因此,元件生產具有廠商內規模回報遞增的性質。從而一種元件只有一個廠商來生產,這一性質被Ethier(1982)稱為“國內規模收益遞增”。由於處於壟斷競爭地位的各品種元件的生產具有對稱性,n種元件的總要素束m投入量為:
元件的均衡產出規模為常數,不受要素稟賦、相對要素價格和相對產品價格等因素的影響。
在封閉均衡狀態下,完全競爭的農業廠商獲得零利潤均衡,則農業的總成本等於總收入,即:
把方程(5)帶入上式,兩邊同除以w,可得:
方程(14)、(16)、(17)和(18)包含4個未知數w、r、m和A,但是這個方程組線性相關,取其最大無關組方程(14)、(17)和(18)可以得出相對要素價格:
結論1:即使存在規模收益遞增的情況,其國內的相對要素價格僅受到要素稟賦、生產技術參數和偏好參數約束,與規模收益遞增參數α無關;並且一個國家的資本-勞動比越大,其相對要素價格(即租金-工資比)將越小。
假設除了要素稟賦不同外,本國和外國其他方面都相同。本文利用上標“*”來表示外國相應變數,從而我們可以繼續分析在自由貿易情況下的國際均衡狀態。
首先,兩國完全競爭的農業廠商把投入要素價格當作給定,可以根據方程(4)給定產量的成本最小化問題和相應的解(方程(5)),寫出兩國農業的投入組合分別為:
最後,自由貿易使得兩國的製造品投入品的品種擴展到:N=n+n[*]。由於每個國家的元件定價相同,因此,無論是本國的還是外國的製造業對本國或外國所生產的各種元件的需求數量相同。但是,由於兩國元件價格不一定相等,則對不同國家元件的均衡需求數量不一定相同。設本國製造業對每種本國元件和外國元件的需求分別為:x[,11]和x[,12],外國製造業對每種本國元件和外國元件的需求分別為x[21,]和x[,22]。從而兩國製造品的生產函式由方程(6)變為:
聯立方程(37)和(38),以及聯立方程(39)和(40),分別可以得出:
結論2:即使在規模收益遞增的情況下,其國際相對要素價格也僅受到世界要素結構、生產技術參數和偏好參數約束,與規模收益遞增參數α無關;並且世界的資本-勞動比越大,其相對要素價格(即租金-工資比)將越小。
把方程(44)代入方程(28)可得:
將上兩式與方程(20)和(21)相比,在國際均衡狀態下,相對於農產品價格的絕對要素價格隨著相對要素價格變化而變化。
利用方程(44)、(45)和(46),可以求解本國的主要經濟變數:元件投入的總要素束和要素束成本價、元件價格q、每種元件的均衡產出水平x、本國農產品的生產量A和消費量A,這些內生變數都是世界要素稟賦、生產技術參數和消費支出份額的函式;只有製造品的數量M、價格P以及對國內外每種元件的需求不僅是上述三個外生變數及參數的函式,也是規模收益遞增參數α的函式。外國也是如此。
如果把要素束m看成初級產品,則根據方程(5)、(9)、(10)和(13),可以得出產品的相對價格與要素相對價格之間的關係:
因此,可以得出如下結論:
結論3:隨著要素相對價格上升,產品的相對價格也上升,要素密集度不會發生逆轉現象。

