定義
設p和q為兩個多項式，次數分別為m和n。因此：
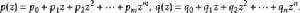西爾維斯特矩陣於是，與p和q相關的西爾維斯特矩陣，就是通過以下方法得到的矩陣{\displaystyle (n+m)\times (n+m)}：
•第一行為：
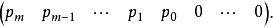西爾維斯特矩陣•第二行是第一行往右移一列；第二行第一列的元素是零。
•下面的(n-2)行也是用這種方法得出，每次都往右移一列。
•第(n+1)行為
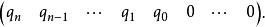西爾維斯特矩陣•餘下的行仍然是每次都往右移一列。
因此，如果我們設m=4和n=3，則矩陣為：
西爾維斯特矩陣套用
西爾維斯特矩陣用於交換代數中，例如測試兩個多項式是否有一個（非常數）公因式。確實，在這種情況下，相關的西爾維斯特矩陣的行列式（稱為兩個多項式的結式）等於零。反過來也成立。
以下線性方程組的解
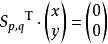西爾維斯特矩陣
西爾維斯特矩陣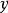
西爾維斯特矩陣
西爾維斯特矩陣
西爾維斯特矩陣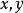
西爾維斯特矩陣
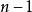西爾維斯特矩陣
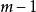西爾維斯特矩陣其中 是大小為 的向量， 是大小為 的向量，由滿足下式的多項式對 （次數分別為 和 ）的係數向量構成：
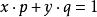西爾維斯特矩陣
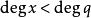西爾維斯特矩陣
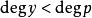西爾維斯特矩陣這就是說，西爾維斯特矩陣的轉置的核給出了裴蜀方程的所有解，其中 且 。
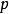西爾維斯特矩陣
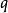西爾維斯特矩陣這樣，西爾維斯特矩陣的秩決定了 和 的最大公因式的次數：
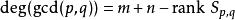西爾維斯特矩陣