西爾維斯特定理

西爾維斯特定理是給出計算矩陣子式的方法的一個命題。西爾維斯特定理又叫西爾維斯特恆等式，由西爾維斯特（Sylvester,J.J.）給出。

西爾維斯特矩陣

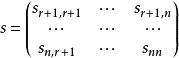西爾維斯特定理

在n階矩陣A=(a)中，取第1,2,...,r,r+i行與第1,2,...,r,r+j列構成一個r+1階矩陣，記為B(i, j=1,2,...,n-r)，令s=|B|，n-r階矩陣 稱為西爾維斯特矩陣。

定理簡介

西爾維斯特定理是給出計算矩陣子式的方法的一個命題。

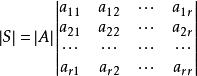西爾維斯特定理

西爾維斯特定理

等式 ，其中 稱為西爾維斯特定理或西爾維斯特恆等式，由西爾維斯特（Sylvester,J.J.）給出。

矩陣子式

矩陣A是一個mXn矩陣, 任取A的k行和k列, 位於這k行和k列交匯點處的k 個元素按原來的順序構成一個k階行列式，這個k階行列式就稱為矩陣A的一個k階子式。