簡介
西北角法是從西北角(左上角)格開始,在格內的右下角標上允許取得的最大數;然後按行(列)標下一格的數;若某行(列)的產量(銷量)已滿足,則把該行(列)的其他格划去;如此進行下去,直至得到一個基本可行解的方法。
西北角法應遵循“優先安排運價表上編號最小的產地和銷地之間(即運價表的西北角位置)的運輸業務”的規則。
舉例
從表1中可知,總的產量=總的銷量,故產銷是平衡的。
第一步:列出運價表和調運物資平衡表。
運用表上作業法時,首先要列出被調運物資的運價表和供需平衡表(簡稱平衡表),如表1,2所示。
| 供\價格\需 |  西北角法 西北角法 |  西北角法 西北角法 |  西北角法 西北角法 |  西北角法 西北角法 |
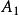 西北角法 西北角法 | 3 | 11 | 3 | 10 |
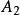 西北角法 西北角法 | 1 | 9 | 2 | 8 |
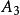 西北角法 西北角法 | 7 | 4 | 10 | 5 |
| 供\需 |  西北角法 西北角法 | 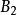 西北角法 西北角法 | 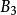 西北角法 西北角法 | 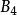 西北角法 西北角法 | 供量(T) |
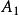 西北角法 西北角法 | 7 | ||||
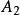 西北角法 西北角法 | 4 | ||||
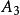 西北角法 西北角法 | 9 | ||||
| 需量(T) | 3 | 6 | 5 | 6 | 20 |
第二步:編制初始調運方案。
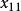 西北角法
西北角法首先在表2的西北角方格(即左上角方格,對應變數),儘可能取最小值:
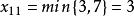 西北角法
西北角法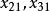 西北角法
西北角法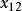 西北角法
西北角法將數值3填入該方格(見表3)。由此可見必須為0,即第一列其他各方格都不能取非零值,划去第一列。在剩下的方格中,找出其西北角方格,
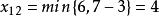 西北角法
西北角法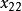 西北角法
西北角法將4填入它所對應方格,第一行飽和,划去該行。再找西北角方格 ,
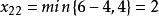 西北角法
西北角法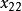 西北角法
西北角法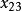 西北角法
西北角法將2填入 所對應方格,於是第二列飽和,划去該列。繼續尋找西北方格為 ,
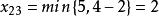 西北角法
西北角法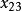 西北角法
西北角法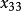 西北角法
西北角法將2填入 所對應方格,第二行飽和,划去該行。剩下方格的西北角方格為 ,
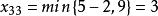 西北角法
西北角法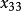 西北角法
西北角法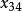 西北角法
西北角法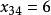 西北角法
西北角法將3填入 所對應方格,第三列飽和,划去該列。最後剩下 方格,取 。
| 供\需 |  西北角法 西北角法 | 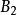 西北角法 西北角法 | 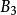 西北角法 西北角法 | 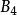 西北角法 西北角法 | 供量(T) |
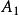 西北角法 西北角法 | 3 | 4 | 7 | ||
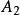 西北角法 西北角法 | 2 | 2 | 4 | ||
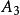 西北角法 西北角法 | 3 | 6 | 9 | ||
| 需量(T) | 3 | 6 | 5 | 6 | 20 |
這樣我們就找到了m+n-1=3+5-1=7個基變數,它們為:
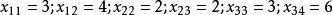 西北角法
西北角法顯然它們用折線連線後不形成閉迴路。這就是西北角法所找初始基可行解。
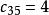 西北角法
西北角法利用西北角法找初始基可行解簡單可行,但也存在問題。例如在表3中可見,單價高於該行其他各方格,最簡單想法是單價小的情況下多運些貨物,這樣總運費會更小些,最小元素法就改進了西北角法的缺點。