基本思路
閉合迴路法是表上作業法的最後的一個步驟,是指當找到運輸問題的一個初始基可行解之後,判定此解是否是最優解的一種方法。
可仿照一般的單純形法,檢驗這個解的各個非基變數(對應運輸表中是的空格)的檢驗數是否都是正數。若有某空格(A,B)的檢驗數為負,說明將x變為基變數將可使目標函式值減少,即使運輸費用減少,故當前這個解不是最優解。若所有空格的的檢驗全非負,則不管怎樣變換解均不能使運輸費用降低,即目標函式值已無法加以改進,這個解即是最優解。
為了計算出運輸表中空格(非基變數)的檢驗數,引入閉迴路的概念,使用閉迴路可以直觀地為滿足約束條件換入變數增值後,再從原來的某一基變數中減去相應數值,變成數值為零的換出變數,完成換入換出即運量的調整。
定律定義
閉迴路
所謂閉迴路,就是指在調運方案表中,從一個空格出發,沿水平或垂直方向前進,遇到一個適當的有數字的格子時,轉90°繼續前進,直到回到起始空格為止,形成一條由水平線段和垂直線段所組成的封閉折線。
求某個空格(非基變數)的檢驗數,就先要找出它在運輸表上的閉迴路,這個閉迴路的頂點由起點的空格和其他均為填有數字的格(基變數格)構成。閉迴路可以是一個簡單的矩形,也可以是有水平和豎直邊線組成的封閉多邊形,下面示出幾種較為簡單的閉迴路的圖形,需要注意的是多邊形是可以交叉的,只要圖形交叉的地方是空格便可。
 閉合迴路法
閉合迴路法 空心圓點表示起點,實心表示經過的基變數,直線穿過空格即非基變數。可以證明,每一個空格(非基變數)一定存在唯一的一條閉迴路。
注意事項
如果有多個檢驗數為負數時,首先要調整的是絕對值最大的負檢驗數對應的空格,它需要將對應的非基變數作為換入變數,變成基變數。若有兩個以上相等的絕對值最大的負檢驗數時,則選對應運費最小的一個非基變數為換入變數,其值從零增加到大於零的正值,即調整運量。
前提條件
在運輸問題基可行解的疊代過程中,不允許出現全部頂點由填有數字的格(基變數格)構成的閉迴路。因為位於閉迴路上的一組變數,他們對應的運輸問題約束條件的係數列向量相關。這就是說,在確定運輸問題的初始基可行解時,要求基變數的個數保證在(m+n-1)個,用西北角法、最小元素法和沃格爾法得到的解都滿足這些條件。由於尋找初始基可行解使用的方法的高明性不同,上述需要使用閉迴路法調整的次數一般來說是依次遞減的。
計算步驟
計算檢驗數
下表即是一個產銷平衡的運輸問題的運輸表並且已使用最小元素法填入了基變數,現利用此初始解說明檢驗數的計算方法。
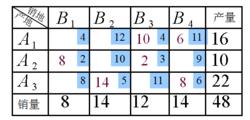 閉合迴路法
閉合迴路法 藍色方框中的是運價,橙色數字是基變數的值。如(A,B)表示從產地A運送8個單位的貨物到銷地B,其運價為2個單位。
首先考慮表中的空格(A,B),構想由產地A供應1個單位的物品給銷地B,為使運入銷地B1的物品總數量不大於它的銷量,就應該將產地A運到B的物品數量減去一個單位,即將格子(A,B)中填入的數字8改為7;為了使由產地A運出的物品正好等於它的產量,且保持新的到的解仍為基可行解,需將x由原來的2增加1,改為3。然後將x13由10減去1,即變為9,以使運入銷地B3的物品數量正好等於它的銷量,同時使由A1運出的物品數量正好等於它的產量。顯然,由於x的的調整將影響到x、x、x這三個變數的取值,即(A,B),(A,B),(A,B),(A,B)這四個格子中填入的數據。在運輸表中,每一個空格都可以和一些有數字的格子用水平線段和垂直線段交替連線在一閉合迴路上,而且這種閉合迴路是唯一的。而且,運輸問題的檢驗數的定義是產地到銷地供給1個單位物品所引起的總運費的變化。非基變數或者說空格(A,B)的檢驗數σ即由此引起的總運費變化是:σ=c-c+c-c=4-2+3-4=1。可以看出在計算檢驗數時,符號在起點時為正,任意時針往下到下個頂點,此時符號為負,由此正負交替直到所有頂點包括進去。
檢驗方案的數據指標,編排各個閉合迴路,這樣的工作熟練可以在。現再看空格(A,B),它的閉迴路的頂點由以下各格組成:(A,B),(A,B),(A,B),(A,B),(A,B),(A,B),最後再回到(A,B)。
在實際操作中由於塗改不便,熟練則可以不用編制各個閉合迴路,在心中假想即可,其檢驗數為σ=c-c+c-c+c-c=10-5+6-11+4-3=1。檢驗數為正數,表明修改這個基變數只會增加總運費,因此觀察其他空格的檢驗數。
按照同樣的方法,可得表中其他的非基變數的檢驗數如下:
σ=c-c+c-c+c=12-5+6-11=2
σ=c-c+c-c=9-11+4-3=-1
σ=c-c+c-c+c-c=8-2+3-4+11-6=10
σ=c-c+c-c+c=11-6-11+4=12
由於σ=-1

