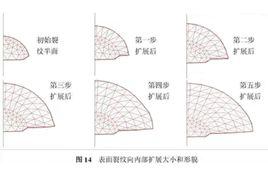
發展歷史
我們知道從1914年英格雷斯（Ingless）和1921年格里菲斯（Griffith）提出斷裂力學開始。一直到60年代都停留線上彈性斷裂力學（LEFM）的層次。後來由於發現裂紋尖端進入塑性區後用斷裂力學（LEFM）仍然無法解決應力奇性（stress singularity）的問題。1960年由巴潤布拉特（Barenblatt）和達格代爾（Dugdale）率先提出了非線性或可塑性斷裂力學（nonlinear/plastic fracture mechnics）的概念，在裂紋前端引入了塑性域（plastic zone），這也就是我們用的結合斷裂力學（cohesive fracture mechnics）的前身。當時這個概念.還沒引起學術界的轟動。直到1966年賴斯（Rice）發現J積分（J-integral）及隨後發現斷裂力學（LEFM）中J積分（J-integral）是等於能量釋放速率（energy release rate）的關係。隨後在工程中發現了越來越多的斷裂力學（LEFM）無法解釋的問題。結合斷裂力學（cohesive fracture mechnics）開始引起更多的關注。在研究以混凝土為代表的準易脆材料（quassi-brittle material）時，I型凝聚斷裂力學（Icohesive fracture mechnics）提供了非常好的結果，所以在70年代到90年代，結合斷裂力學（cohesive fracture mechnics）被大量套用於混凝土研究中。比較常用的方法主要是虛擬裂紋方法（fictitious crack approach）和有效彈性裂紋方法（effective-elastic crack approach）或是稱為等效彈性裂紋方法（equivalent-elastic crack approach）。其中虛擬裂紋方法（fictitious crack approach）只考慮了達格代爾-巴潤布拉特能源機制（Dugdale-Barenblatt energy mechanism）而有效彈性裂紋方法（effective-elastic crack approach）只考慮了基於斷裂力學（LEFM）的格里菲斯-伊文能源損耗機制（Griffith-Irwin energy dissipation mechanism）。但作了一些修正。
分類及階段
根據裂紋受載情況可以劃分為三類基本模式：張開型裂紋（Mode I）、剪下型裂紋（Mode II）和撕開型裂紋（Mode III）。
裂紋擴展往往經歷成核、穩態擴展和失穩擴展三個階段，裂紋擴展一旦進入失穩擴展將對材料使用性能造成不可逆損傷，其危害性極大。
公式
相關計算如圖（圖一、圖二、圖三、圖四）所示。
圖一動能與裂紋擴展阻力
圖二失穩斷裂的裂紋擴展率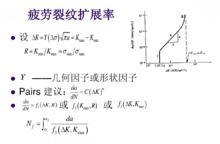
圖三疲勞裂紋擴展率（1）
圖四疲勞裂紋擴展率（2）分析方法
做裂紋有限元分析（abaqus）有幾種常見方法。
用debond命令
最簡單的是用debond命令，定義*FRACTURE CRITERION，TYPE=XXX，參數。
*DEBOND，SLAVE=XXX，MASTER=XXX，time increment=XX 0，1，
time，00
要想看到開裂特別注意需要在指定的開裂路徑上定義一個*Nset。 然後在*INITIAL CONDITIONS，TYPE=CONTACT中定義master，slave，及指定的Nset這種方法用途其實較為有限。
interaction模組
另一種方法，在interaction模組，special，定義crack seam，格線最好細化，用collapse element模擬singularity。這種方法可以計算J積分，應力強度因子等常用的斷裂力學參數裂尖及奇異性定義在interaction-special，先定義crack，定義好裂尖及方向，然後在singularity選擇：midside node parameter：輸入0.25，然後選Collapsed element side，duplicate nodes。 8節點單元對應（1/r） （1/r^1/2）奇異性。這裡midside node parameter選0.25對應裂尖collapse成1/4節點單元。如果midside nodes不移動到1/4處，則對應（1/r）奇異性，適合perfect plasticity的情況.
裂尖格線劃分
格線劃分：裂尖格線劃分有一些技巧需要注意。
partition後先處理最外面的正方形。 先在對角線和邊上布點。 記住要點constraint，然後選第三個選項do not allow the number of elements to change不準seed變化，密度可以自己調整.最裡面靠近圓的正方形可以只在對角線上布點.也可以進一步分割內圓及在圓周上布點.裡面裂尖周圍的內圓選free mesh，element type選cps6或者cpe6，外面四邊形選sweep mesh，element type選cps8或者cpe8，記住把quad下那個縮減積分的勾去掉。
注意事項
這種方法的幾個值得注意的問題。
主要是對斷裂力學的理解問題。
1.為什麼設定理想彈塑性（epp）分析的時候得到的xx，yy方向或者最大應力值Sxx，Syy會超過材料的屈服強度Sy呢，這分析結果可能嗎?
這是因為在有限元分析（abaqus）中對應等於材料的屈服強度的是von Mises等效應力Se=Sy。 因此在平面應變的條件下，xx方向的應力Sxx=Sy*pi/SRQT（3）Sy，而Syy=Sy*（2 pi）/SRQT（3），大概是3倍的屈服應力。所以得到大於材料的屈服強度的xx及yy方向應力是正常的。
2.為什麼設定collapse element的時候對彈性分析在中間就一個點而要把單元邊上的中點移到1/4處，但彈塑性分析卻要在中間設定一圈點並且保持單元邊上的中點位置不變呢?
這個其實不是隨便定的，在有限元中分析裂紋時。
對彈性分析需要模擬裂尖1/SQRT（r）的奇異性，這樣在把單元邊上的中點移到1/4處後計算出來的等參單元拉格郎日型函式對應的u field正好包含1/SQRT（r）項，事實上這一方法在斷裂力學的數值模擬發展史上是很巧妙的一個發現。
仍然被廣泛採用。至於理想彈塑性分析需要模擬裂尖1/r的奇異性，這樣大家都知道在把單元邊上的點放在到1/2處後計算出來的正常的等參單元拉格郎日型函式對應的ufield包含1/r項，可以模擬彈塑性分析需要的裂尖1/r的奇異性。所以在看似動手點幾下就能實現的分析模式後面有很清楚漂亮的理論作支持
也可以使用python控制seam尺寸，然後移動partition和格線。
還有就是比較新的cohesive element單元。我仔細讀了有限元分析（abaqus） cohesive element的理論幫助，個人意見有限元分析（abaqus）的cohesive element採用的是廣泛套用於混凝土的類似fictitious crack的方法。只考慮了Dugdale-Barenblatt energy mechanism。這其中softening law的影響是非常重要的。但ABAUQS似乎只提供了linear或者exponential的softening law，複雜的本構關係還需要另想辦法。至於基於Griffith-Irwin energy dissipation mechanism的J-integral值可以在LEFM分析中單獨算。（有限元分析（abaqus）用的是Suo Zhigang和Hutchinson在1990一篇論文中提出的方，cohesive fracture mechnics已經被套用於各種材料。不過在使用到納米或者更小數量級的研究中碰到了不少問題。
可能需要結合位錯和分子動力學的一些理論。現有的cohesive element單元需要定義damage initiation和evolution的準則，softening準則好像只有linear和exponential。但對一般材料也夠用了。然後通過設定後處理display group可以看到裂紋擴展情況。裂紋擴展不是有限元分析（abaqus）的強項，比較方便的只能用cohesive element。做過幾個模型效果還可以，但對應的參數需要一定的實驗數據支持。
否則做出來了也不知道對不對。要注意geometric thickness和constitutive thickness；material stiffness和interfacial stiffness的區別以及厚度與精度的影響。Cohesive element的核心主要是TS-Law，無論裡面的數據如何選取。
厚度如何變化，cohesive element的表現取決於TS-Law的定義。具體dava的popo10已經給過詳細的解釋的討論。
自己可以編寫cohesive Uel，以便更加靈活的定義cohesive element的T-S law，基本流程如下。
Abquas可以做3d裂紋擴展，不能作mode III的裂紋擴展，因為理論上沒有mode III的裂紋擴展準則。三維的斷裂力學準測，MODE I本身就是1D問題沒什麼好說的，MODE II已經解決咯，你可以用subroutine寫進去。而MODE III的斷裂界面有分層問題，沒有任何人給出合理解釋，因為MODE III本身是全三維問題，原有的斷裂力學的準則，必須引入新的一個新的尺度參數，但是還沒有接過，所以有限元分析（abaqus）也是沒有的，這有限元分析（abaqus）也是承認的。用coh模擬裂紋擴展，也是要大體上了解可能產生crack的位置和它將會擴展的路線。理論上cohesive zone model可以解決更廣泛的問題，有限元分析（abaqus）6.5版本開始引進的cohesive element，開發進一步的套用可能需要一段時間。
至於2D是三個類型都有的，這是有限元分析（abaqus）手冊原話：
Crack propagation： The crack propagation capability allows quasi-static crack growth along predefined paths to be studied in two-dimensional cases （“Crack propagation analysis，” Section 11.4.3）. Cracks debond along user-defined surfaces. Three crack propagation criteria are available， and multiple cracks can be included in the analysis. Contour integrals can be requested in crack propagation problems.
基本思想就是：部分或全部結合（cohesive）單元沾合成一個斷裂模型，因為裂紋驅動機制，比如體積應變之類。 沾合的模型就沒有了制定路徑，體積應變的驅動機制受到3咯方向主應變影響，則體積應變分布就比應力分布相對複雜，隨機性就自然孕育其中。這樣的樣基本思想實在有限元分析（abaqus）的動態斷裂模擬下完成的，動態斷裂的應力波擾動也會影響到驅動機制。
本構模型
有限元分析（abaqus） 用連續介質的方法建立描述混凝土模型 不採用巨觀離散裂紋的方法描述 裂紋的水平的在每一個積分點上單獨計算其中。
低壓力混凝土的本構關係包括：
Concrete Smeared cracking model （abaqus/Standard） ，
Concrete Brittle cracking model （abaqus/Explicit），
Concrete Damage plasticity model，
高壓力混凝土的本構關係：
Cap model
1、有限元分析（abaqus）/Standard中的彌散裂縫模型Concrete Smeared cracking model （abaqus/Standard）：
——只能用於有限元分析（abaqus）/Standard中。
裂紋是影響材料行為的最關鍵因素，它將導致開裂以及開裂後的材料的各向異性。
用於描述 ：單調應變 、在材料中表現出拉伸裂紋或者壓縮時破碎的行為。
在進行參數定義式的Keywords：
*CONCRETE，
*TENSION STIFFENING，
*SHEAR RETENTION，
*FAILURE RATIOS，
2、有限元分析（abaqus）/Explicit中脆性破裂模型Concrete Brittle cracking model （abaqus/Explicit） ：
適用於拉伸裂紋控制材料行為的套用或壓縮失效不重要，此模型考慮了由於裂紋引起的材料各向異性性質，材料壓縮的行為假定為線彈性，脆性斷裂準則可以使得材料在拉伸應力過大時失效。
在進行參數定義式的Keywords：
*BRITTLE CRACKING，
*BRITTLE FAILURE，
*BRITTLE SHEAR，
3、塑性損傷模型Concrete Damage plasticity model：
適用於混凝土的各種荷載分析，單調應變， 循環荷載，動力載荷，包含拉伸開裂（cracking）和壓縮破碎（crushing），此模型可以模擬硬度退化機制以及反向載入剛度恢復的混凝土力學特性
在進行參數定義式的Keywords：
*CONCRETE DAMAGED PLASTICITY
*CONCRETE TENSION STIFFENING
*CONCRETE COMPRESSION HARDENING
*CONCRETE TENSION DAMAGE
*CONCRETE COMPRESSION DAMAGE
裂紋建模要點
1、裂紋的有限元分析關鍵在於格線的劃分，在有限元分析（abaqus）裡面單元的塌陷是由有限元分析（abaqus）自己來完成的，用戶要做的只是劃分格線，這可不是一件容易的事情。
2、格線劃分：其實我們的目的是為了得到在裂紋區域很密的單元，而在其他區域較疏鬆，同時在裂紋的周圍n（取決於自己定義圍線積分的計算層數）層單元必需用六面體單元。我們通常的做法是用"蜘蛛網"形式來實現這種格線的疏密過渡，請注意，特別在有限元分析（abaqus）裡面格線的過渡過程參數設定不合適，造成過程區域格線的扭曲經常會導致格線的劃分失敗，因此需要大家多試試!
3、單元選擇：單元的選擇大多數的資料上都有，強調一點就是我們一般要選擇高次單元。這裡要說的是有限元分析（abaqus）劃分時單元的定義問題，我們知道在裂紋線的周圍我們我們是用六面體單元，但要坍塌成楔形，剛開始的時候將單元形狀設為楔形，然後設定單元類型的時候他總是顯示成楔形，而不是六面體，後來發現，其實這一步是多餘的，只要先定義好了裂紋，再劃分單元，有限元分析（abaqus）會自動將楔形單元轉為六面體單元；
4、未穿透頭裂紋問題的處理：當裂紋線終止於模型內部時，三維時我們會遇到一個問題，就是在裂紋線的末端，存在一個有裂紋和沒有裂紋的分界線，如果我們按照一般的方法處理，在沒有裂紋的區域，有限元分析（abaqus）會將無裂紋區域與裂紋區第一層坍塌單元的過渡單元設成楔形，這樣六面體坍塌單元和楔形單元共用節點，有限元分析（abaqus）會提示錯誤：裂紋區域不能用楔形、三角形單元。所以，遇到這樣的問題，將模型一分為二，然後tie，就可以解決這個問題了。
5、因為我們斷裂力學的理論本身就有很大的爭議，最大的問題是奇異性在實際中是不可能出現的，理論上的奇異是由於我們認為裂紋無限尖造成的，這是不複合實際的。而且實際材料中的裂紋並不是我們所假設的理想結構比如橢圓，因此我們建議大家在做這一塊時務必小心，看我們的處理是不是合適，是不是能說明問題。
