定義
ARMA模型(auto regressive moving average model)自回歸滑動平均模型，模型參量法高解析度譜分析方法之一。這種方法是研究平穩隨機過程有理譜的典型方法，適用於很大一類實際問題。它比AR模型法與MA模型法有較精確的譜估計及較優良的譜解析度性能，但其參數估算比較繁瑣。
ARMA模型參數估計的方法很多：
如果模型的輸入序列{u(n)}與輸出序列{a(n)}均能被測量時，則可以用最小二乘法估計其模型參數，這種估計是線性估計，模型參數能以足夠的精度估計出來；
許多譜估計中，僅能得到模型的輸出序列{x(n）}，這時，參數估計是非線性的，難以求得ARMA模型參數的準確估值。從理論上推出了一些ARMA模型參數的最佳估計方法，但它們存在計算量大和不能保證收斂的缺點。因此工程上提出次最佳方法，即分別估計AR和MA參數，而不像最佳參數估計中那樣同時估計AR和MA參數，從而使計算量大大減少。
基本原理
將預測指標隨時間推移而形成的數據序列看作是一個隨機序列，這組隨機變數所具有的依存關係體現著原始數據在時間上的延續性。一方面，影響因素的影響，另一方面，又有自身變動規律，假定影響因素為x1，x2，…，xk，由回歸分析，
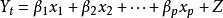ARMA模型其中Y是預測對象的觀測值，Z為誤差。作為預測對象Yt受到自身變化的影響，其規律可由下式體現，
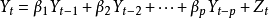ARMA模型誤差項在不同時期具有依存關係，由下式表示，
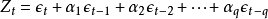ARMA模型由此，獲得ARMA模型表達式：
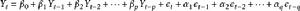ARMA模型基本形式
ARMA模型分為以下三種：
自回歸模型（AR：Auto-regressive）
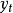ARMA模型如果時間序列
滿足
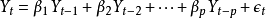ARMA模型
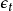ARMA模型其中
是獨立同分布的隨機變數序列，且滿足：
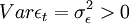ARMA模型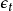ARMA模型以及 E(
) = 0
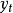ARMA模型則稱時間序列
為服從p階的自回歸模型。
自回歸模型的平穩條件：
滯後運算元多項式
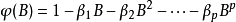ARMA模型的根均在單位圓外，即φ(B) = 0的根大於1。
移動平均模型（MA：Moving-Average）
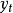ARMA模型如果時間序列
滿足
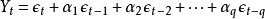ARMA模型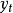ARMA模型，則稱時間序列
為服從q階移動平均模型；
移動平均模型平穩條件：任何條件下都平穩。
自回歸滑動平均模型（ARMA）
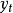ARMA模型如果時間序列
滿足：
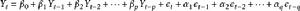ARMA模型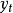ARMA模型則稱時間序列
為服從(p,q)階自回歸滑動平均混合模型。或者記為φ(B)
= θ(B)
AR模型
AR 模型(auto regressive model)自回歸模型，模型參量法高解析度譜分析方法之一，也是現代譜估計中常用的模型。
用AR模型法求信具體作法是：
①選擇AR模型，在輸入是衝激函式或白噪聲的情況下，使其輸出等於所研究的信號，至少，應是對該信號的一個好的近似。
②利用已知的自相關函式或數據求模型的參
數。
③利用求出的模型參數估計該信號的功率譜。
MA模型
MA模型(moving average model)滑動平均模型，模型參量法譜分析方法之一，也是現代譜估中常用的模型。
用MA模型法求信號譜估計的具體作法是：①選擇MA模型，在輸入是衝激函式或白噪聲情況下，使其輸出等於所研究的信號，至少應是對該信號一個好的近似。②利用已知的自相關函式或數據求MA模型的參數。③利用求出的模型參數估計該信號的功率譜。
在ARMA參數譜估計中，大多數估計ARMA參數的兩步方法都首先估計AR參數，然後在這些AR參數基礎上，再估計MA參數，然後可求出ARMA參數的譜估計。所以MA模型參數估計常作為ARMA參數譜估計的過程來計算。
套用
可以用於處理分離正弦信號頻率，多套用於機械零件比如齒輪、軸承故障診斷和分析。
