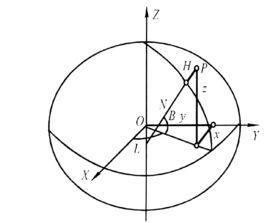
產生原因
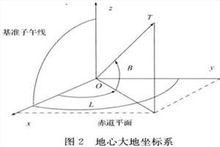 地心坐標系
地心坐標系20世紀50年代之前,一個國家或一個地區都是在使所選擇的參考橢球與其所在地區的大地水準面最佳擬合的條件下,按弧度測量方法來建立各自的局部大地坐標系的。由於當時除海洋上只有稀疏的重力測量外,大地測量工作只能在各個大陸上進行,而各大陸的局部大地坐標系間幾乎沒有聯繫。不過在當時的科學發展水平上,局部大地坐標系已能基本滿足各國大地測量和製圖工作的要求。但是,為了研究地球形狀的整體及其外部重力場以及地球動力現象;特別是50年代末,人造地球衛星和遠程彈道武器出現後,為了描述它們在空間的位置和運動,以及表示其地面發射站和跟蹤站的位置,都必須採用地心坐標系。因此,建立全球地心坐標系(也稱為世界坐標系)已成為大地測量所面臨的迫切任務。
建立方法
第一類是重力測量方法,它是利用重力測量資料,按斯托克斯公式和韋寧-邁內茲公式全球積分,聯同天文坐標得出大地原點或若干地麵點的地心大地坐標 ( L, B, H)。但由於重力資料在全球分布還很不均勻,多數地區還相當稀疏,按此法所得地心大地坐標精度目前僅約為10米以內。
第二類是衛星大地測量方法,這又可分為衛星動力法和衛星定位法。 衛星動力法是單獨利用人造衛星觀測資料或綜合人造衛星和地面大地測量觀測資料,按動力法原理同時解算出地球重力場模型和全球分布的若干地面跟蹤站的地心坐標。例如,美國戈達德空間飛行中心(GSFC)的地球重力場模型GEM-10至GEM-10C等,都包括全球146個跟蹤站的地心大地坐標,法國和聯邦德國聯合研究的地球重力場模型GRIM-3,包括95個跟蹤站的地心大地坐標。這兩種模型地心坐標的精度約為1~5米。衛星定位法是利用地面站接收機接收某種導航衛星的信息,直接測定地面接收站的地心大地坐標。例如美國海軍導航衛星系統(NNSS)或全球定位系統 (GPS)所測定的地心坐標。
第三類方法是綜合利用全球地面大地測量資料和人造衛星觀測資料組成新型弧度測量方程,推求局部坐標系對地心坐標系的轉換參數。根據轉換參數就可把局部坐標系換算為地心坐標系。換算公式是:
r = r0+(1+ m) Rr′,
式中 r是測點的地心坐標矢量; r0是局部坐標系原點的地心坐標矢量; r′是測點在局部坐標系中的位置矢量; m是尺度改正數; R是一個鏇轉矩陣,它的元素是獨立的歐拉角 εx、 εy、 εz,表示圍繞局部坐標系 x、 y、 z軸的鏇轉。計算這些轉換參數至少要有3個公共點,它們在兩種坐標系中的位置都是已知的。
目前由此法所得地心坐標轉換參數的精度可達1~3米。
建立地心坐標系的第一類經典重力測量方法,由於目前全球重力資料還不足,故所得坐標精度還較低,但隨著全球重力資料的增加,其精度還會提高。第二類方法可以直接得出跟蹤站或接收站的地心坐標。第三類則可利用轉換參數將局部大地坐標系中任一大地點的坐標換算為地心坐標系中的相應數值。