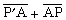衍射的幾何理論
正文
套用射線概念分析電磁波衍射特性的漸近理論，簡稱 GTD。幾何理論是單色波場方程的解在頻率趨於無限時的極限,因而也是適合於高頻情形的漸近解,而這種理論的基本思想是把均勻平面波在無限平界面上的反射和折射、在半無限楔形導體邊緣上的衍射和沿圓柱導體表面的爬行波嚴格解的漸近式，套用於從點源發出的球面波或線源發出的柱面波在圓滑界面上的反射和折射、在弧形導體刃口上的衍射和沿導體凸表面的爬行，並把它作為問題的0階段近解。這種解法包括三個方面的計算：
① 射線描述。當源點P┡和場點P的位置已定時,由P┡點到達 P點的反射線和衍射線應當是一條極值線。根據這條原則來判定反射點、衍射點和爬行線。在弧形刃上衍射時（圖1）,如
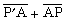比
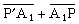和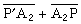
都大或都小，A 點就是衍射點，這點的切線P┡A和 PA的夾角一定相同。在凸曲面上衍射時,如圖2, P┡A、P┡A1、P┡A2、和PB、PB1、PB2都是到曲面的切線,如果
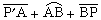比相鄰的兩條路徑都短，則
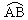就是爬行線，這條短程線是兩端固定在P┡和P的繃緊橡皮筋的自然形狀。 
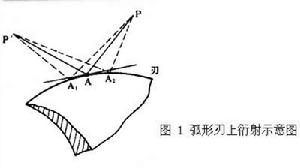衍射的幾何理論
衍射的幾何理論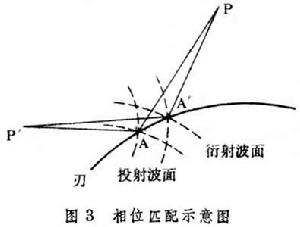
衍射的幾何理論③ 投射波、反射波和衍射波的場強各與其主曲率半徑的幾何平均數成反比，而確定反射波和衍射波曲率矩陣的原則是相位匹配。所謂相位匹配,如圖3，設A是衍射點，A┡是其鄰點，則，A、A┡兩點所在的衍射波面的相位差與 A、A┡兩點所在的投射波面的相位差應當相同。
衍射的幾何理論最早是由J.B.凱勒於1957年提出來的，後來經許多人的工作而日趨完善，在處理很多異形物體的散射問題以及用數值計算解散射和衍射問題中得到套用。但是，因為嚴格解的漸近式在陰影區與照明區的過渡區域不能成立，所以在這個區域，GTD 不能套用，為了彌補這一缺陷，J.波斯馬等人後來提出一致漸近理論 (UAT)。這個理論的基本思想是，給投射波乘以人為因子,使這因子在照明區內近於1而在陰影區內近於0,在過渡區內則隨著場點趨近於照明區邊界而無限增大。將這乘了因子的投射波與衍射波的漸近式相加能一致連續，這種理論也得到了廣泛的套用。但是，它的基礎僅僅是一個估值(ansatz),而且在刃口以及其他焦散線附近,它和 GTD同樣不能套用。然而射線理論有很多優點，人們仍在探索改進的途徑。
