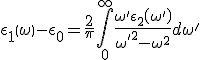色散關係

色散關係（dispersion relation）是指物理學中從因果律出發（與其他 原理相結合）得出的積分關係式的統稱。色散關係作為因果律的推論，主要思想可概括為：設外界對某一物理系統輸入信號（或施加作用），作為反應系統產生輸出信號（或次級作用）。只要此系統具有下述性質：①內部運動規律不隨時間改變；②輸入和輸出按因果方式聯繫；③輸出是輸入的線性泛函，則可求出此線性泛函的傅立葉變換的解析性質，進而得到可測量間的積分關係式——色散關係。

概念說明

推導色散關係時只用到因果律和其他一些普遍原理，而無須對系統內部運動規律或相互作用項作具體的說明或假定。所得色散關係式中都是可直接與物理測量相聯繫的量。因此色散關係在物理學許多領域中獲得廣泛的套用。

理論詮釋

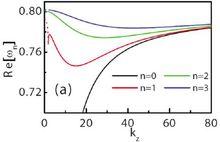金屬納米線上之表面電漿子的色散關係

對色散關係的研究，從討論經典電磁理論中電介質的折射率隨電磁波頻率的變化開始。由經典電子論得知，介質中的電磁波由入射波和從各散射中心發出的散射波相干疊加而成。一個合理的假定是認為這樣的物理系統具有上面的三個性質。這時因果律體現在要求入射波碰到散射中心以前，散射波振幅為零。從這點出發得出介質折射率作為頻率的函式的解析性質，導出了克拉末－克朗尼格公式，即介質折射率的色散關係式。它將折射率的實部用其虛部（即介質對電磁波的吸收係數）對頻率的積分關係式表出。對於絕緣介質，這關係式兩邊都可直接測量，曾經利用它研究了經典電子論中許多問題。後來M.蓋耳－曼、M.戈德伯格等人進一步討論了量子電動力學中的色散關係問題。

量子場論和基本粒子理論中關於色散關係的研究，集中在20世紀50年代中期到60年代初期這一段時間。主要原因一方面是由於微擾理論不能用到強相互作用領域，人們亟待尋找新的可靠的方法；而另一方面是用色散關係研究問題時，只要求遵從一些普遍有效的原理，而無須對強作用動力學機制（相互作用拉格朗日量）作出具體的假定。這點非常適應於當時量子場論和基本粒子物理的發展狀況。關於量子場論中色散關係的證明問題，至今沒有徹底解決。只有當體系中粒子質量滿足一定不等式而動量轉移數值限定在一定範圍時，單重色散關係才能得到嚴格的證明。而對於雙重色散關係，即使在微擾論框架下，也只有某些特殊過程的散射振幅能滿足曼德爾施塔姆表象中關於解析性的要求。

具體研究

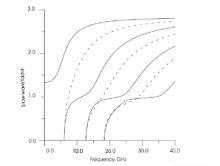電磁波色散關係

量子場論中散射振幅可表為場算符的推遲對易子在物理態間矩陣元的傅立葉變換式。通過運動學分析它又可分解成一些標量函式，可以認為它們是解析函式在其複數變數趨於實數軸時的邊界值。利用微觀因果性對場算符對易子的約束，討論出散射振幅中這些標量函式的解析性質，並利用柯西定理，就可導出有關的色散關係。
兩粒子彈性散射振幅是粒子能量和動量轉移的二元函式，一般的散射振幅是多元函式，如果固定或積分掉其他變數只留下一個變數（例如能量）變動，得到的關係稱為單重色散關係式，以別於後來進一步假定散射振幅能同時對於兩個變數（例如能量和動量）作解析延拓後，提出的曼德爾施塔姆表象或所謂雙重色散關係。
最簡單的色散關係把向前彈性散射振幅的實部表示為正比於其虛部（與粒子散射過程的總截面相聯繫）的函式對能量的積分、對向前彈性散射色散關係的實驗檢驗也檢驗了微觀因果性。

　用色散關係研究強作用時，是將解析性與么正性、譜條件、交叉對稱性等相結合，使得到的許多物理過程的散射振幅相互聯繫，得出一組耦合的方程式。利用它們可以對強作用進行唯象分析。50年代中後期到60年代初期，用這種方法對於低能π介子及核子（N）的作用進行了大量研究，包括分析π－N散射實驗數據，討論它的（3，3）共振態的效應、估算π－π作用的影響，並由此研究了核子電磁形狀因子、低能時在核子上的光生、電生 π介子等一系列問題。與此同時還利用色散關係討論了散射過程的高能極限問題，得出了一些重要的結果，它們之中值得提出的是強作用中粒子和反粒子總截面在高能時趨於同一極限的坡密朗丘克定理和限定總截面隨能量增長速率的弗魯瓦薩爾上限。由於推導它們時只涉及到一些普遍有效的原理，因此這些結論被認為是正確、可靠的。
配合色散關係研究的另一個影響，是促進了量子力學和量子場論中對於散射振幅（包括產生振幅）解析性的更加深入的研究，爾後在這種研究熱潮中，提出了強作用唯象學中產生重要作用的雷其極點理論。
60年代中後期，強作用理論研究主流之一是流代數，人們將色散關係與流代數結合後，又得出了一些重要的結果。這包括與矢量流守恆 （CVC）、軸矢流部分守恆（PCAC）有關的一些結果、阿德勒－韋斯伯格求和規則和其他一些低能定理等。