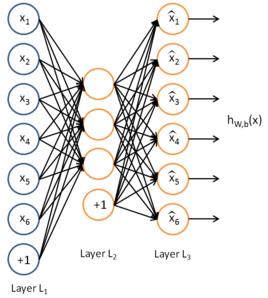
簡介
自編碼器(Autoencoder,AE)是一個3層或者大於3層的神經網路,將輸入表達X編碼為一個新的表達Y,然後再將Y解碼回X。這是一個非監督學習算法,使用反向傳播算法來訓練網路使得輸出等於輸入。當向網路中添加一些限制時,可以學到一些關於輸入表達的有趣結構。當隱含層節點數d比輸入層節點數n小時,可以得到一個輸入的壓縮表達。當d比n大時,添加一些限制,比如稀疏限制,會得到類似於稀疏編碼的結果。
發展
自編碼器的想法一直是神經網路歷史景象的一部分 (LeCun, 1987; Bourlard and Kamp, 1988; Hinton and Zemel, 1994)。傳統自編碼器被用於降維或特徵學習。近年來,自編碼器與潛變數模型理論的聯繫將自編碼器帶到了生成式建模的前沿。自編碼器可以被看作是前饋網路的一個特例,並且可以使用完全相同的技術進行訓練,通常使用小批量梯度下降法(其中梯度基於反向傳播計算) 。不同於一般的前饋網路,自編碼器也可以使用再循環(recirculation)訓練 (Hinton and McClelland, 1988),這種學習算法基於比較原始輸入的激活和重構輸入的激活。
欠完備自編碼器:從自編碼器獲得有用特徵的一種方法是限制h的維度比x小,這種編碼維度小於輸入維度的自編碼器稱為欠完備(undercomplete)自編碼器。學習欠完備的表示將強制自編碼器捕捉訓練數據中最顯著的特徵。
正則自編碼器:編碼維數小於輸入維數的欠完備自編碼器可以學習數據分布最顯著的特徵。我們已經知道,如果賦予這類自編碼器過大的容量,它就不能學到任何有用的信息。如果隱藏編碼的維數允許與輸入相等,或隱藏編碼維數大於輸入的過完備(overcomplete)情況下,會發生類似的問題。在這些情況下,即使是線性編碼器和線性解碼器也可以學會將輸入複製到輸出,而學不到任何有關數據分布的有用信息。理想情況下,根據要建模的數據分布的複雜性,選擇合適的編碼維數和編碼器、解碼器容量,就可以成功訓練任意架構的自編碼器。正則自編碼器提供這樣的能力。正則自編碼器使用的損失函式可以鼓勵模型學習其他特性(除了將輸入複製到輸出),而不必限制使用淺層的編碼器和解碼器以及小的編碼維數來限制模型的容量。這些特性包括稀疏表示、表示的小導數、以及對噪聲或輸入缺失的魯棒性。即使模型容量大到足以學習一個無意義的恆等函式,非線性且過完備的正則自編碼器仍然能夠從數據中學到一些關於數據分布的有用信息。
稀疏自編碼器一般用來學習特徵,以便用於像分類這樣的任務。稀疏正則化的自編碼器必須反映訓練數據集的獨特統計特徵,而不是簡單地充當恆等函式。以這種方式訓練,執行附帶稀疏懲罰的複製任務可以得到能學習有用特徵的模型。由於自編碼器的潛在表示y是對於輸入x的一種有損壓縮。最佳化和訓練只能讓它對於訓練集合來說是很好的壓縮表示,但並不是對於所有的輸入都是這樣。為了增加隱藏層的特徵表示的魯棒性和泛化能力,引入去噪自編碼器。
去噪自編碼器在自編碼器的基礎上,在輸入中加入隨機噪聲再傳遞給自編碼器,通過自編碼器來重建出無噪聲的輸入。加入隨機噪聲的方式有很多種。該過程隨機的把輸入的一些位(最多一半位)設定為0,這樣去噪自編碼器就需要通過沒有被污染的位來猜測被置為零的位。能夠從數據的抽樣部分預測整體數據的任何子集是在該抽樣中能夠找到變數聯合分布的充分條件(Gibbs抽樣的理論依據),這說明去噪自編碼器能夠從理論上證明潛在表示能夠獲取到輸入的所有有效特徵。
特徵表達及數據降維
特徵表達及數據降維真實世界中存在大量非常複雜的事物和現象,通常我們希望能夠以一種更加簡潔且完整的方式去表示一個事物或現象,這就需要去揭示隱藏在複雜表象下的事物或現象的客觀規律。從某個事物或現象(例如天氣狀況)中抽象出一些數據(如溫度、濕度、風力等),通過多個變數來表示或描述一個現象,這個多維變數叫做特徵。特徵作為機器學習系統的原材料,對於最終模型的影響毋庸置疑。機器學習算法的性能在很大程度上取決於數據表達或特徵表達的選擇,當數據能夠被很好地表達為特徵時,即便使用簡單的模型也可達到滿意的精度。故在實際套用機器學習算法時,很重要的一個步驟是怎樣預處理數據以得到一個好的特徵表達。真實世界中的數據通常是高維的。對高維數據的處理包括兩點特性。第一點是“維數災難”,它給後面的數據處理帶來困難,是處理高維數據時遇到的最大問題之一;第二點是“維數福音”,高維數據中包含著關於客觀事物和現象的極為全面和豐富的信息,蘊含著解決問題的可能性,當然也含有很多冗餘信息。作為一類普遍存在的規律,在大多數情況下我們觀察到的從表面上看是高維的、複雜的事物或現象,實際上是可以用少量的簡單變數來支配的。處理高維數據的關鍵是在眾多的因素中找到事物的本質規律。在圖像處理領域,原始像素值作為初級特徵表達時通常維度很高,需要採用合適的降維方法對圖像高維特徵進行處理,以得到更加簡潔而有效的特徵表達。數據降維技術可以克服“維數災難”,在模式識別、數據挖掘、機器學習等領域都具有廣泛套用,相應研究方興未艾 。