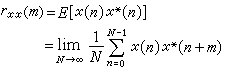正文
自相關函式是隨機信號在不同時刻的值之間的依賴性的量度,是一個很有用的統計平均量,其定義為自相關函式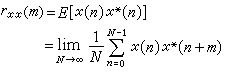 (1)
(1)
在隨機信號處理中,自相關函式可以用來檢測淹沒在隨機噪聲干擾中的信號,隨機信號的自功率譜等於它的自相關函式的傅立葉變換。因此,通過自相關估計可求得信號的功率譜。
利用計算機計算自相關估值有兩種方法。一種是直接方法,先計算出隨機信號和它的滯後序列的乘積,再取其平均值即得相關函式的估計值。另一種是間接方法,先用快速變換算法計算隨機序列的功率譜密度,再作反變換計算出相關函式。
直接算法 設離散隨機信號序列x(n)是平穩的,其長度為N,自相關函式的估值記作惲Nx(m),定義為
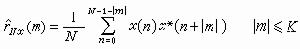 (2)
(2)
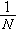 改成
改成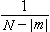 ,即令
,即令 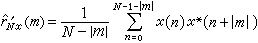
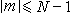 (3)
(3)
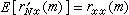 ,因而是無偏的估計。顯然,設m為有限值,當N→∞,則從式(2)可以得到漸近無偏估計。計算m 個滯後數時的自相關估計約需Nm 次實數乘加運算。
,因而是無偏的估計。顯然,設m為有限值,當N→∞,則從式(2)可以得到漸近無偏估計。計算m 個滯後數時的自相關估計約需Nm 次實數乘加運算。 間接算法 間接方法是利用快速傅立葉變換的方法計算出功率譜密度函式的估值,然後再計算它的傅立葉反變換,即得自相關函式估值。由於採用了快速傅立葉變換算法,計算速度較快。如當N=2P時,間接算法所需要的運算量約為8NP次實數乘加運算。因此,兩種方法的速度比是
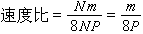
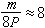 ,即間接算法比直接算法約快8倍。在用間接算法計算相關函式時,需要把隨機信號序列的長度補零擴大到2N-1之後再計算其相關函式。
,即間接算法比直接算法約快8倍。在用間接算法計算相關函式時,需要把隨機信號序列的長度補零擴大到2N-1之後再計算其相關函式。 參考書目
何振亞:《數位訊號處理的理論與套用》下冊,人民郵電出版社,北京,1983。
J.S.Bendat et al. ,Random Data: Analysis and Measurement Procedures,Wiley-Interscience,New York,1971.