廣義矩估計法的提出與發展
廣義矩方法(generalized method of moments GMM)是關於參數估計的一種原理,關於GMM的一般表述是由漢森(1982)提出的。GMM最大的優點是僅需要一些矩條件而不是整個密度。很多的估計量都可以視為GMM的特例,這些估計量包括普通最小二乘估計量、工具變數法估計量、兩階段最小二乘估計量、非線性聯立方程系統的估計量以及動態理性預期模型的估計量等,在很多情況下即使極大似然估計量也可看作是GMM的一個特例。許多計量經濟學的模型不是通過完全的分布假設而是通過矩條件來設定,例如帶有不可觀測的個體影響的動態平面數據模型和含有理性預期的微觀經濟模型,這些模型通常是使用GMM方法來估計的。
GMM方法的提出促進了金融計量經濟學的發展,金融計量經濟學的發展也為GMM方法提供了更為廣闊的套用空間,同時也推動了GMM理論的完善。金融計量經濟學(Financial Econometrics)是隨著經濟學的發展而產生的一門新的分支學科,它在已開發國家也只有十餘年的歷史,而在中國則是剛剛提出的。金融計量經濟學的發展除了得益於金融經濟學的發展外,還得益於以下兩個重要原因:一是特殊的計量經濟方法的發展。70年代末和80年代初C.W.J.Granger和R.F.Engle創立了協整回歸模型(Cointegration),R.F.Engle和J.Cragg發展了條件自回歸異方差模型(ARCH),以及Hansen(1982)提出的GMM估計方法。這些在金融市場計量領域有著特殊套用價值的計量分析工具極大地推動了金融計量經濟學的發展;二是金融市場數據採集預處理技術的發展。現代科學技術的進步特別是通訊和計算機技術的進步使得大量的金融即時數據可以及時獲得,豐富與相對完整的金融數據使得深受數據貧乏困擾的計量經濟學一旦轉向金融領域就有了可以大顯身手的用武之地。值得注意的是我國的國情以及金融環境與西方不同,因此不可能照搬照抄,必須要在借鑑西方先進理論的基礎上針對我國自己的情況進行實際修正。只有這樣才能建立具有中國特色的金融計量經濟學理論。
GMM方法對非線性數據處理的研究起著重要的作用。金融計量學方法對金融數據的處理多採用線性結構,但經濟行為從許多方面表現出非線性關係,而且變數的數目也在增加。經驗表明投資者對風險和預期收益的態度是非線性的;證券市場所有參與者的行為,以及信息通過證券價格反映出來的過程都是非線性的。因此金融計量經濟學研究的前沿是非線性問題的建模與估計,而在這兩方面中模型的估計越來越成為金融計量經濟學的焦點,也成為制約著定量分析的關鍵,GMM估計法就是在這樣的背景下越來越受到人們的關注,它的理論日趨完善套用日漸廣泛,這一方法的大樣本性質已有較好的結果,它大大突破了原矩法的局限性,而且在相當大的範圍內具有極大似然估計的優良性,其計算是離不開計算機的。動態系統理論,非線性時間序列分析。隨機波動模型,估計方法以及非參數統計學的發展,推動了金融數據非線性化的研究,在這一領域中GMM都起到了非常重要的作用。雖然我國對GMM的研究還處於起步階段,但是國外的很多計量經濟學家一直關注其理論的發展和套用的推廣,並對此作了很多研究,同時也對我國研究GMM估計法提供了很多方向。
基本思想
在隨機抽樣中,樣本統計量將依機率收斂於某個常數。這個常數又是分布中未知參數的一個函式。即在不知道分布的情況下,利用樣本矩構造方程(包含總體的未知參數),利用這些方程求得總體的未知參數。
廣義矩估計是統計學和計量經濟學中常用的一種半參數估計方法,Lars Peter Hansen1982年根據Karl Pearson1894年發明的矩估計(method of moments)發展而來。GMM的發明是Hansen得到2013年諾貝爾經濟學獎的原因之一。
GMM的產生主要使用時機是最小二乘法的嚴格假設條件不成立時(例:解釋變數與誤差項有相關性),並且不知道資料的機率分布,以致不能使用最大似然估計時,GMM方法的寬鬆假設使得它在計量經濟學(Econometrics)中得到廣泛套用。
GMM估計法具有一致性、漸近常態分配,有效率等性質。
估計方法描述
 廣義矩估計
廣義矩估計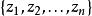 廣義矩估計
廣義矩估計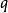 廣義矩估計
廣義矩估計假設我們有個來自某統計模型的觀測值,並且我們知道下列個矩(moment)條件成立,
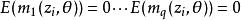 廣義矩估計
廣義矩估計 廣義矩估計
廣義矩估計 廣義矩估計
廣義矩估計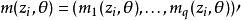 廣義矩估計
廣義矩估計 廣義矩估計
廣義矩估計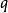 廣義矩估計
廣義矩估計其中,是一個關於該統計模型的維未知參數。另外,定義成關於的維矩函式。所以,我們有條件
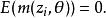 廣義矩估計
廣義矩估計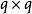 廣義矩估計
廣義矩估計 廣義矩估計
廣義矩估計給定一個的權重矩陣,我們自然有
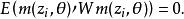 廣義矩估計
廣義矩估計 廣義矩估計
廣義矩估計 廣義矩估計
廣義矩估計由此,關於未知參數的GMM估計量是
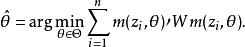 廣義矩估計
廣義矩估計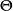 廣義矩估計
廣義矩估計 廣義矩估計
廣義矩估計其中,是參數的取值空間。
優點
傳統的計量經濟學估計方法,例如普通最小二乘法、工具變數法和極大似然法等都存在自身的局限性。即其參數估計量必須在滿足某些假設時,比如模型的隨機誤差項服從常態分配或某一已知分布時,才是可靠的估計量。而GMM 不需要知道隨機誤差項的準確分布信息,允許隨機誤差項存在異方差和序列相關,因而所得到的參數估計量比其他參數估計方法更有效。因此,GMM 方法在模型參數估計中得到廣泛套用。

