定義
給定n階線性定常系統
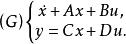 能檢測性
能檢測性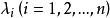 能檢測性
能檢測性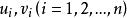 能檢測性
能檢測性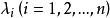 能檢測性
能檢測性設 A的特徵值為,稱為系統(G)的 極點。設分別為的左特徵向量和右特徵向量,即
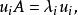 能檢測性
能檢測性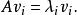 能檢測性
能檢測性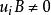 能檢測性
能檢測性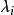 能檢測性
能檢測性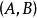 能檢測性
能檢測性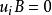 能檢測性
能檢測性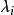 能檢測性
能檢測性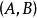 能檢測性
能檢測性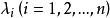 能檢測性
能檢測性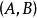 能檢測性
能檢測性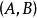 能檢測性
能檢測性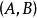 能檢測性
能檢測性如果,則稱為的 能控極點;如果,則稱為的不能控極點。如果所有均為能控極點,則稱為 能控的;如果的所有不能控極點均具有負實部,則稱為能穩定的。
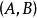 能檢測性
能檢測性能穩定的等價條件為:
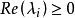 能檢測性
能檢測性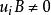 能檢測性
能檢測性(1) 若,則。
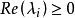 能檢測性
能檢測性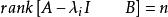 能檢測性
能檢測性(2) 若,則。
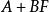 能檢測性
能檢測性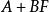 能檢測性
能檢測性(3) 存在適當選擇的矩陣F,使得成為穩定陣,即的特徵值均具有負實部。
(4) 若存在相似變換,使得
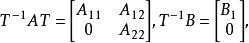 能檢測性
能檢測性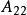 能檢測性
能檢測性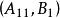 能檢測性
能檢測性則為穩定陣,是能控的。
類似地,可定義能 檢測性如下。
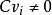 能檢測性
能檢測性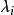 能檢測性
能檢測性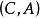 能檢測性
能檢測性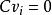 能檢測性
能檢測性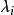 能檢測性
能檢測性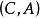 能檢測性
能檢測性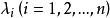 能檢測性
能檢測性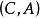 能檢測性
能檢測性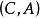 能檢測性
能檢測性如果,則稱為的 能觀測極點;如果,則稱為的不能觀測極點。如果所有均為能觀測極點,則稱(C,A)為 能觀測的,如果的所有不能觀測極點均具有負實部,則稱為 能檢測的 。
能檢測的等價條件
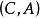 能檢測性
能檢測性能檢測的等價條件為:
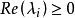 能檢測性
能檢測性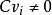 能檢測性
能檢測性(1) 若,則。
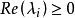 能檢測性
能檢測性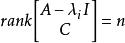 能檢測性
能檢測性(2) 若,則
 能檢測性
能檢測性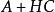 能檢測性
能檢測性(3) 存在適當選擇的矩陣,使得成為穩定陣。
(4) 若存在相似變換,使得
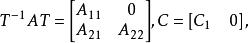 能檢測性
能檢測性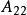 能檢測性
能檢測性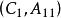 能檢測性
能檢測性則是穩定陣,能觀測。
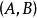 能檢測性
能檢測性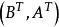 能檢測性
能檢測性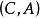 能檢測性
能檢測性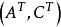 能檢測性
能檢測性此外,如果能穩定,則能檢測;如果能檢測,則能穩定。反之亦然 。

