定義
能控性資料在狀態空間模型中，通常系統的輸出可以直接量測到，但系統的全部狀態一股不能直接獲取．那么，一個自然的問題是：能否由觀測到的輸出軌跡將系統的狀態儘可能準確地確定出來?對於確定性的微分方程或差分方程狀態空間方程模型，在控制信號給定時（主要：控制信號可視為已知)，由於任意時刻的狀態都由初始狀態決定，所以問題轉換為能否由系統的輸出軌跡來確守初始狀態．
控制系統大多採用反饋控制的形式。在現代控制理論中，其反饋信息是由系統的狀態變數組
合而成的。但並非所有的系統狀態變數在物理上都可測，於是就有了能否通過對輸出的測量來獲取全部狀態變數信息的問題，即線性系統的能觀性問題。
並非所有狀態變數都是可測量或有物理意義的，因此提出能否通過可測量的輸出量y獲得系統的狀態量，這便是系統的能觀測性問題。
若系統S對於T0時刻，存在Ta時刻，即T0<Ta，根據[T0，Ta]時刻上的y(t)測量值能夠地確定系統在T0時刻的初始狀態X0，則稱X0為系統在[T0，Ta]區間上的能觀狀態。
若T0時刻的任意初始狀態X0都是能觀的，則稱系統S在T0時刻是完全能觀的。
若T0也是任意的，則稱系統是完全能觀的。
狀態能觀性的定義
對線性系統而言,狀態能觀性只與系統的輸出y(t),以及系統矩陣A和輸出矩陣C有關,與系統的輸入u(t)和輸入矩陣B無關,
即討論狀態能觀性時,只需考慮系統的自由運動即可，
因為矩陣A,B,C和輸入u(t)均已知,故上式的右邊第二項可以計算出來,也是已知項。
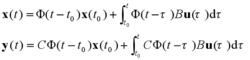狀態和輸出的解研究狀態能觀性問題,即為上式對任意的初始狀態x(t0)能否由輔助輸出y-(t)來確定的問題。
所以線性系統狀態能觀性僅與輸出y(t),以及系統矩陣A和輸出矩陣C有關,與輸入矩陣B和輸入u(t)無關。
也就是說,分析線性系統的能觀性時,只需考慮齊次狀態方程和輸出方程即可。
能觀性判據
1 矩陣指數函式判據
判定方法：矩陣函式的各列函式線性獨立
特點：需要求矩陣指數函式並判定函式相關,計算複雜
2 代數判據
現代控制理論判定方法：能觀性矩陣滿秩
特點：計算簡便可行。缺點為不知道狀態空間中哪些變數(特徵值/極點)能觀
3 模態判據1
判定方法：約旦標準形中同一特徵值對應的C矩陣分塊的第一列線性無關
特點：易於分析狀態空間中哪些變數(特徵值/極點)能觀。缺點為需變換成約旦標準形
能觀性的直觀討論
狀態能觀性反映系統外部可直接或間接測量的輸出y(t)和輸入u(t)來確定或識別系統狀態的能力。
如果系統的任何內部運動狀態變化都可由系統的外部輸出和輸入確定,那么稱系統是能觀的,
或者更確切地說,是狀態能觀的。否則,就稱系統為狀態不完全能觀的。
能控性和能觀性
能控性和能觀性是相對的概念。
動態系統的能控性和能觀性是揭示動態系統不變的本質特徵的兩個重要的基本結構特性。
卡爾曼在60年代初首先提出狀態能控性和能觀性。其後的發展表明,這兩個概念對回答被控系統能否進行控制與綜合等基本性問題,對於控制和狀態估計問題的研究,有著極其重要的意義。
系統能控性指的是控制作用對被控系統的狀態和輸出進行控制的可能性。
能觀性反映由能直接測量的輸入輸出的量測值來確定反映系統內部動態特性的狀態的可能性。
