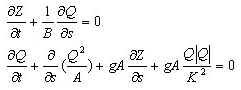聖維南方程組
正文
描述水道和其他具有自由表面的淺水體中漸變不恆定水流運動規律的偏微分方程組。由反映質量守恆律的連續方程和反映動量守恆律的運動方程組成。1871年由法國科學家A.J.C.B.de聖維南提出,故名。一百多年來,雖然為了考慮更多的因素和實際套用方便對它的基本假定作了某些簡化或改進,產生出多種不同的表達形式,但其實質沒有變化。主要進展表現在求解方法的改進和創新。1877年法國工程師克萊茨提出了瞬態法。1938年蘇聯С.А.赫里斯季安諾維奇提出另一類解法──特徵線法。但均因計算量較大,不得不進行各種簡化處理,使實際套用受到限制。自50年代以來,隨著電子計算機的普及,研究和提出了一整套解法,並研究出若干個通用性較強的套用軟體(即程式系統),促進了聖維南方程組在水文和其他工程領域中的套用。
方程組的形式 一維單寬水流情況下,聖維南方程組的典型形式為:
式中t為時間;s 為距水道某固定斷面沿流程的距離;h、v、Z0分別為相應於s處過水斷面的水深、斷面平均流速和水底高程;Hf為由於摩阻損失而引起的能量比降;g為重力加速度;t和s為自變數;h和v為因變數;Z0、Hf可由s、h和v確定。(1)式為連續方程,反映了水道中的水量平衡,即蓄量的變化率(第一項)應等於沿程流量的變化率(第二項)。 (2)式為運動方程。其中第一項反映某固定點的局地加速度,第二項反映由於流速的空間分布不均勻所引起的對流加速度。以上兩項稱為慣性項。第三項反映由於底坡引起的重力作用,稱為重力項。第四項反映了水深的影響,稱為壓力項。第三、四項可合併為一項,即水面比降。第五項為水流內部及邊界的摩阻損失。該式表達了重力與壓力的聯合作用使水流克服慣性力和摩阻引起的能量損失而獲得加速度。
聖維南方程組還有許多其他形式。例如:以斷面流量代替流速,以面積代替水深作為因變數;也可考慮河道兩側的沿程入流、地轉力和水面風力的影響;還可把垂線平均流速作為因變數,寫出二維水體漸變不恆定明流的運動方程。
基本假定 建立聖維南方程組的基本假定是:①流速沿整個過水斷面(一維情形)或垂線(二維情形)均勻分布,可用其平均值代替。不考慮水流垂直方向的交換和垂直加速度,從而可假設水壓力呈靜水壓力分布,即與水深成正比;②河床比降小,其傾角的正切與正弦值近似相等;③水流為漸變流動,水面曲線近似水平。此外,在計算不恆定的摩阻損失Hf時,常假設可近似採用恆定流的有關公式,如曼寧公式(見河水運動)。
聖維南方程組描述的不恆定水流運動是一種淺水中的長波傳播現象,通常稱為動力波。因為水流運動的主要作用力是重力,屬於重力波的範疇。如忽略運動方程中的慣性項和壓力項,只考慮摩阻和底坡的影響,簡化後方程組所描述的運動稱為運動波。如只忽略慣性項的影響,所得到的波稱為擴散波。運動波、擴散波及其他簡化形式可以較好地近似某些情況的流動,同時簡化計算便於實際套用。
求解方法 聖維南方程組在數學上屬於一階擬線性雙曲型偏微分方程組。聯解方程組並使其符合給定的初始條件和邊界條件,就可得出不恆定水流的流速和水深(或其他因變數)隨流程和時間的變化,即v=v(s,t)和h=h(s,t)。初始條件為某一起始時刻的水流狀態,如水道沿程各斷面的水深和流速。邊界條件為所計算的水體的邊界水流狀態,如某一河段上、下游邊界斷面處的水位過程、流量過程或水位流量關係等。給定的初始條件和邊界條件的數目和形式必須恰當,符合水流的性質,才能保證方程組的解存在和唯一,保證不致因數據的微小變化而使方程的解發生很大的變化。此時,問題稱為是適定的,求解才有意義。
除特殊情況外,很難用解析方法求得聖維南方程組的解析解。一般只能通過數值計算獲得個別情況的近似解。常用的數值計算方法主要有以下三類:①有限差分法。將所計算的水體按照一定的格線劃分,每個格線點處的微分形式的聖維南方程組,用某種形式的差分方程組來逼近。邊界條件也寫成差分形成。然後逐時段地求解差分方程組,得出各格線點(如斷面)處的水深及流速。根據所採用的差分計算方法的不同,對每一計算時段來說,或可逐個算出各格線點處的水力要素,或是必須聯立求解各網點處的水力要素。前者稱為顯式差分法,後者稱為隱式差分法。克萊茨提出的瞬態法就屬於一種簡化的顯式差分法。②特徵法。把聖維南方程組由偏微分方程組變換為在所謂“特徵”上成立的常微分方程組,通常稱為特徵方程組。在空間為一維的情況下,“特徵”的幾何表示稱為特徵線,而在二維則為特徵面。不恆定水流中的波動和干擾是沿“特徵”傳播的。用有限差分法聯立求解表達“特徵”幾何位置的方程和特徵方程組,即可求得所需的數值解。③有限單元法。把水體劃分成幾何形狀簡單的單元(如一維的直線段,二維的矩形、直邊或曲邊三角形等),在每一單元內,解用數學處理比較簡單的內插函式來逼近。把聖維南方程組套用於每個單元,變換為積分形式,並根據某種準則(如逼近的殘差最小)來確定內插函式中的待定係數便可定解。常用的是伽遼金半離散有限單元法。
除了求解完全或簡化形式的聖維南方程組的上述解法,在水文學中多年來還對一維流動發展出許多簡化計算方法。例如,把運動方程簡化為計算時段內計算河段的蓄水量與出流量之間關係的方程,然後聯立求解。同時,已對水文學中常用的方法與求解聖維南方程組的關係進行了研究。如套用廣泛的馬斯金格姆(曾譯“馬斯京根”)流量演算法,可列為擴散波中的特殊情形。水文學方法簡單,而且能較好地適用於某些情況,今後仍將長期廣泛地被套用。
對於非漸變的流動,水流通過激波把兩部分漸變流連線起來。如通過水躍實現由急流(超臨界流)到緩流(次臨界流)的過渡。在漲潮和潰壩波中也常出現近乎垂直的波前。此時,兩邊的漸變流仍可用聖維南方程組來描述。只要補充激波處的跳躍條件和用以判別物理上是否許可的某種準則(如熵條件等)即可求解。
聖維南方程組所描述的具有自由表面的水體的漸變不恆定流動的計算具有重要的實際意義。洪流演進計算是洪水預報、堤防設計和防洪系統運用的重要依據。水電廠引水渠、下游尾水、灌溉和通航水道中的不恆定流計算,是確定堤岸、尾水管出口高程,論證發電、航運、給水等工程設施的安全和效益的根據。此外,潮汐河口的潮流計算、潰壩決堤造成的洪水災害的估計等也都具有十分重要的經濟意義。
參考書目
V.Yevjevich,K.Mahmood,ed.,Unsteady Flow in Open Channels,Vol.1,Water Resources Publ.,Fort Collins,Colorado,1975.