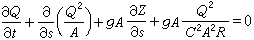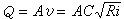明渠流
正文
具有顯露於大氣中的自由水面的水流,如天然河道、人工渠道中的水流。明渠的流量、斷面形式、坡度、糙率等的變化,都會引起自由水面的變化,相應地也使水深和流速變化。自由水面的計算是工程中需解決的一個重要問題,如引水或排水渠道的合理斷面尺寸和流速大小的決定,攔河築壩以後水庫淹沒範圍的估算,都歸結為明渠流水面曲線的繪製。明渠的渠身形狀和大小保持不變的長直渠道稱為稜柱形渠道;斷面形狀和大小沿程變化的渠道稱為非稜柱形渠道。
明渠恆定均勻流 在順直稜柱形長渠道中可形成渠中水深、流速沿程不變的均勻流。均勻流水力計算式:
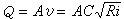
在工程設計中,有時要求在給定斷面面積A的條件下,使渠道通過最大的流量。從上式看出,當n、A、i一定時,要使流量Q極大,必須水力半徑R極大,即濕周極小。使渠道水力半徑為極大的斷面,稱為水力最佳斷面。通常渠道的斷面為梯形。梯形水力最佳斷面滿足如下條件:
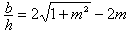
無壓管道(如下水道)具有某些水力特點。如直徑為b的圓形斷面管道,並非剛剛充滿管道時的流量或流速為最大,而是水深h=0.95b時的流量最大;h=0.81b時的流速最大。這是因為過水斷面面積A及水力半徑R與水深h的關係並非單調變化所引起。
明渠恆定非均勻流 在渠道底坡、斷面或糙率等沿程變化的渠道中,必然形成水深、流速沿程變化的非均勻流。
稜柱形渠道非均勻漸變流水深h沿流程s的變化,可由伯努利方程和連續性方程得到如下的規律:
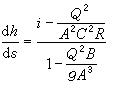
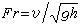 稱為弗勞德數。當Fr<1時,渠道某處水流(如水深)的變化可影響該處上下游,這種水流稱為緩流;當Fr>1時,某處水流的變化只波及下游而不影響上游,這種水流稱為急流。對上式積分,即可求出水深沿流程的分布,即水面曲線,相應可求各斷面的流速。求得水深及流速沿程的變化,即可解決有關工程問題。非稜柱形渠道的水面曲線可用差分法解伯努利方程及連續性方程得到。
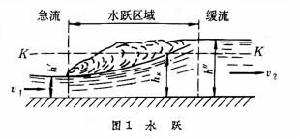
稱為弗勞德數。當Fr<1時,渠道某處水流(如水深)的變化可影響該處上下游,這種水流稱為緩流;當Fr>1時,某處水流的變化只波及下游而不影響上游,這種水流稱為急流。對上式積分,即可求出水深沿流程的分布,即水面曲線,相應可求各斷面的流速。求得水深及流速沿程的變化,即可解決有關工程問題。非稜柱形渠道的水面曲線可用差分法解伯努利方程及連續性方程得到。 水躍 是明渠水流從急流過渡到緩流狀態時水面突然躍起的局部水力現象(圖1,hK為臨界水深)。
 明渠流
明渠流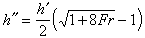
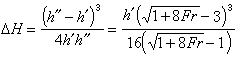
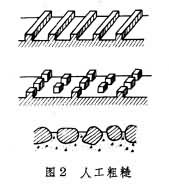
消能 在堰閘下游,陡坡渠道的尾端,橋涵出口,跌水處等水流的流速很大,會沖刷河床,危及建築物的安全。為了把引起沖刷的水流能量在較短的區域內消除,設計有各種消能的措施,如增加渠底粗糙度的人工粗糙(圖2)和利用水躍消能而建的消力池(圖3)等。
 明渠流
明渠流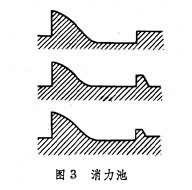 明渠流
明渠流