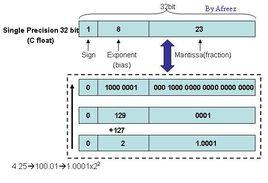
存儲格式
符號位S(sign) - 1bit
首位0代表正號，首位1代表負號。（只有+0，沒有-0）
指數位E(exponent) - 8bit
E的取值範圍為0-255（無符號整數），雙精度為11位，擴張型大於等於15位，實際數值e=E-127。
有時E也稱為“移碼”，或稱為“階碼”
尾數位M(mantissa) - 23bit
M也叫有效數字位（significant）、係數位（coefficient），甚至被稱作“小數”。
在一般情況下，m=（1.M)2，使得實際起作用範圍為1≤尾數<2。
為了對溢出進行處理，以及擴展對接近0的極小數值的處理能力，IEEE 754對M做了一些額外規定，參見後文介紹。
浮點數
對於內部存儲數據（00111111）2：
符號位
（最左側）S=0。這表示是個正數
指數
（左側第2-9位）E=(01111110）2=（126）10，所以e=E-127=-1。
尾數
（最後的23位）M=（11001100110）2，m=（1.M)2=（1.7999999523162841796875）10
該二進制小數轉為10進制的計算方式為1 + （1/2+1/4） + （1/32+1/64） + （1/512+1/1024）……
實際值
N=1.7999999523162841796875*2^-1=0.89999997615814208984375
（其實，這個數據是0.9的單精度浮點數的實際內部存儲，可以看到有一定的誤差）
這裡繼續給出另外幾個數字的實例：
使用豎線|將各個段位分隔顯示
實際值 | 符號位 | ；指數 | ；尾數
1 |
2 |
-6.5 | 1 | 10000001 | 10100000000
表示範圍
單精度最大表示範圍：單精度浮點數可以表示的範圍為±3.40282 * 10^38（1.1111...1×2^127）
接近於0的最小值：單精度浮點數可以表示1.175 * 10-38（1.00...0×2^-126）的數據而不損失精度。
當數值比以上值小的時候，將會由於尾數的有效位數減少而逐步喪失精度（IEEE 754的規定），或者有的系統則直接採用0值來簡化處理過程。
精度
單精度浮點數的實際有效精度為24位二進制，這相當於 24*log102≈7.2 位10進制的精度，所以平時我們說“單精度浮點數具有7位精度”。（精度的理解：當從1.000...02變化為1.000...12時，變動範圍為2^23，考慮到因為四捨五入而得到的1倍精度提高，所以單精度浮點數可以反映2^24的數值變化，即24位二進制精度）
誤差
浮點數以有限的32bit長度來反映無限的實數集合，因此大多數情況下都是一個近似值。同時，對於浮點數的運算還同時伴有誤差擴散現象。
特定精度下看似相等的兩個浮點數可能並不相等，因為它們的最小有效位數不同。
由於浮點數可能無法精確近似於十進制數，如果使用十進制數，則使用浮點數的數學或比較運算可能不會產生相同的結果。
如果涉及浮點數，值可能不往返。值的往返是指，某個運算將原始浮點數轉換為另一種格式，而反向運算又將轉換後的格式轉換回浮點數，且最終浮點數與原始浮點數相等。由於一個或多個最低有效位可能在轉換中丟失或更改，往返可能會失敗。
標準格式
單精度浮點數用4位元組存儲， 雙精度浮點數用8位元組存儲，分為三個部分：符號位、階和尾數。階即指數，尾數即有效小數位數。單精度格式階占8位，尾數占24位，符號位1位，雙精度則為11為階，53位尾數和1位符號位。
細心的人會發現，單雙精度各部分所占位元組數量比實際存儲格式多了一位，的確是這樣，事實是，尾數部分包括了一位隱藏位，允許只存儲23位就可以表示24位尾數，默認的1位是規格化浮點數的第一位，當規格化一個浮點數時，總是調整它使其值大於等於1而小於2，亦即個位總是為1。例如1100B，對其規格化的結果為1.1乘以2的三次方，但個位1並不存儲在23位尾數部分內，這個1是默認位。
階以移碼的形式存儲。對於單精度浮點數，偏移量為127（7FH），而雙精度的偏移量為1023（3FFH）。存儲浮點數的階碼之前，偏移量要先加到階碼上。前面例子中，階為2的三次方，在單精度浮點數中，移碼後的結果為127+3即130（82H），雙精度為1026（402H）。
浮點數有兩個例外。數0.0存儲為全零。無限大數的階碼存儲為全1，尾數部分全零。符號位指示正無窮或者負無窮。
下面舉幾個例子：
單精度浮點數
十進制 ；規格化 ；符號 ；移階碼 尾數
-12 -1.1x2^3 1 1000001
0.25 1.0x2^-2 0 01111101
所有位元組在記憶體中的排列順序，intel的cpu按little endian順序，motorola的cpu按big endian順序排列。
更多規範
0值
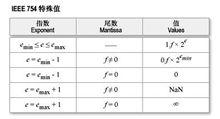IEEE754以指數E、尾數M全零來表示0值。當指數位S變化時，實際存在“正0”和“負0”兩個內部表示，其值認為都等於0。
接近於0的數值
當指數E為0時，IEEE 754規定：m=(0.M)2 e=-126。通過這個規則，將擴大對0值附近數據的表示能力。
幾個實例：
符號S 指數E 尾數M 代表意義 對應10進制 相對誤差 0 00000000.12*2-126 5.87e-39 2-23
000000000 0.012*2-126 2.94e-39 2-22
…… ；…… ；…… ；……
.0000...12*2-126=2-148 2.80e-45 50%
0 1.40e-45 100%
（註：部分系統不支持此類數據，而直接進行0值處理）
存儲變形
單精度浮點數存儲格式單精度浮點數 應廣泛，而一些低成本的單片機系統中不具備數學運算的協處理器硬體，因而在在不同系統中，根據硬體特性對浮點數的軟體實現進行了相應調整和簡化。存在如下一些IEEE 754常見變形：
高低位的位元組順序不同
即高位元組在先的big endian和低位元組在先的little endian。後者在Intel、Motorola等的CPU中大量使用。
指數部分被單獨存為一位元組
獨立位元組比較便於處理。此類系統會把符號位與尾數結合起來存放。
此外，不同系統中對於下列特性可能有細微差異：
無窮大、NaN的規定和處理
這可能會影響到溢出特性
非歸一化數據的處理
有可能為了簡單，而將無法歸一化的小數值直接以0來處理；有的則直接採用（0.M)2方案表示全域尾數，以犧牲1位二進制精度的代價換取算法的同意。
以上兩部分的改變，對大多數的套用情形影響不大。
無窮大
當指數E為全1時，IEEE 754規定此類存儲作為特別使用，而不是普通數據。
無窮大
E=255 M=0時，用作無窮大（或Infinity、∞）。根據符號不同，又有+∞、－∞。
無窮大可以由算術運算得出，下面是有關無窮大的幾個運算示例：
1/∞ = 0,-1/∞ = -0,1/0 = ∞，-1/0 = -∞
NaN
E=255、M不為0時，用作NaN（Not a Number，“不是數”之意）。
當對數據進行非法運算（例如對-1開平方）時，結果出現NaN。
運算時含有NaN時，結果也必定是NaN。
注意：NaN<>NaN！對NaN進行相互比較是無意義的。
（NaN還有QNaN和SNaN的用法，用於程式捕獲某些例外狀態。參見NaN條目）
雙精度
簡介
單精度和雙精度數值類型最早出現在C語言中（比較通用的語言裡面），在C語言中單精度類型稱為浮點類型（float），顧名思義是通過浮動小數點來實現數據的存儲。這兩個數據類型最早是為了科學計算而產生的，他能夠給科學計算提供足夠高的精度來存儲對於精度要求比較高的數值。
但是與此同時，他也完全符合科學計算中對於數值的觀念：
當我們比較兩個棍子的長度的時候，一種方法是並排放著比較一下，一種方法是分別量出長度。但是事實上世界上並不存在兩根完全一樣長的棍子，我們測量的長度精度受到人類目測能力和測量工具精度的限制。從這個意義上來說，判斷兩根棍子是否一樣長絲毫沒有意義，因為結果一定是False，但是我們可以比較他們兩個哪個更長或者更短。這個例子很好地概括了單精度/雙精度數值類型的設計初衷和存在意義。
基於上述認識，單精度/雙精度數值類型從一開始設計的時候，就不是一個準確的數值類型，他只保證在他這個數值類型的精度之內是準確的，精度之外則不保證，比方說，一個數值5.1，很可能存儲在單精度/雙精度數值中的實際值是5.1或者5.09999999999999。導致這個現象的原因我們可以通過兩種方式來解釋：
解釋方法
你可以嘗試在任何一個控制項的屬性面板中，設定他的寬度為：3.2CM，當你輸入完畢後，你會發現值自動變成了3.199cm，無論你怎么改，你都無法輸入3.200CM，因為實際上在電腦中存儲的並不是CM為單位的數值，而是“緹”為單位的數值，而“緹”和CM之間的比值，是個很難被除盡的數，因此你輸入完畢後，電腦自動轉換成了最接近的“緹”值，然後再轉換成厘米顯示到屬性面板上，這一乘一除，兩次四捨五入，誤差就出來了。單精度/雙精度也是類似的原理，其實在 二進制存儲的時候，單精度/雙精度都採用了類似相近分數的方法，而這樣的存儲是不可能做到準確的。
評價
通過解剖 單精度數值的二進制存儲格式，我們可以清楚看到，實際上單精度/雙精度的存儲，都要通過乘法和除法，其中必有捨入，如果恰好你的數值在除法中被捨入了，那么你賦的初值就很可能與你最終存儲的值不完全相同，其中的微小差異，並不與單精度/雙精度的設計目標相違背。
當我們在資料庫中或者VBA代碼中使用一個單精度/雙精度數值的時候，也許你從界面上看不到區別，但是在實際的存儲中，這個差別卻真真切切地就在那裡，當你對其進行相等比較的時候，系統只是簡單地作二進制的比較，界面上無法體現的微小差異，在二進制比較面前卻無處遁形，於是，你的等於比較返回了一個意料之外的False。
