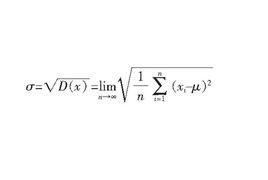定義
總體標準偏差是無窮多次測量情況下的實驗標準偏差,又稱為理論標準差。計算公式為:
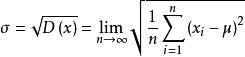 總體標準偏差
總體標準偏差只有當n充分大(例如取n為200以上)的情況下,σ才與s接近,但決不能相等。一般課本或專業書籍上, 往往把σ稱為標準偏差。通常,σ是未知的,S只能作為σ的估算值。而且, 由於n的次數有限,s本身也有個不確定度。
公式推導
標準偏差是一組數值自平均值分散開來的程度的一種測量觀念。一個較大的標準偏差,代表大部分的數值和其平均值之間差異較大;一個較小的標準偏差,代表這些數值較接近平均值。
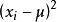 總體標準偏差
總體標準偏差總體標準偏差σ值小,表明測量值比較集中,σ值大表明測量值比較分散。其中, 的目的是為避免正誤差和負誤差相互抵消,因而取其絕對值,開方的目的是為了不改變其量綱。
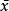 總體標準偏差
總體標準偏差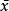 總體標準偏差
總體標準偏差可用標準偏差表征測量值的分散程度, 例如用標準偏差表征測量儀器的重複性和復現性。σ是無限次測量的誤差的正均方根值,但它不是一個具體的誤差。式 -μ=δ,實際上真值是不可知的,一般以算術平均值來作為真值μ的最佳估計值。因此,可以用 代替μ,而用s作為總體標準偏差σ的估計值,此時有:
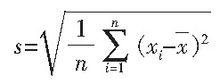 總體標準偏差
總體標準偏差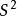 總體標準偏差
總體標準偏差 總體標準偏差
總體標準偏差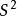 總體標準偏差
總體標準偏差 總體標準偏差
總體標準偏差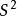 總體標準偏差
總體標準偏差現在的問題是,S是否就是σ的無偏估計值。為了解決這個問題只要計算一下 的數學期望是否是 。如果計算得到 的數學期望是 ,那么就說明S就是σ的無偏估計值,否則就不是。為了計算方便,先把 寫成下面的形式:
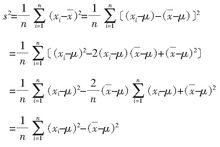 總體標準偏差
總體標準偏差則有:
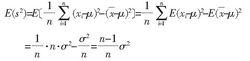 總體標準偏差
總體標準偏差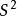 總體標準偏差
總體標準偏差 總體標準偏差
總體標準偏差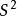 總體標準偏差
總體標準偏差 總體標準偏差
總體標準偏差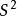 總體標準偏差
總體標準偏差 總體標準偏差
總體標準偏差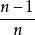 總體標準偏差
總體標準偏差 總體標準偏差
總體標準偏差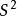 總體標準偏差
總體標準偏差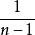 總體標準偏差
總體標準偏差由此可見, 的數學期望並不等於 ,因此 不是 的無偏估計值。如果用 來估計 ,必然在結果中含有一個系統誤差 。為了得到參數 的無偏估計值,只要把 乘以 就可以了,這就是說:
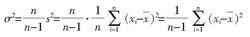 總體標準偏差
總體標準偏差 總體標準偏差
總體標準偏差其中, 稱為總體方差。為了區別總體標準偏差,用S作為總體標準偏差σ的無偏估計值,則有:
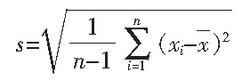 總體標準偏差
總體標準偏差 總體標準偏差
總體標準偏差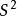 總體標準偏差
總體標準偏差這就是著名的貝塞爾公式。對同一被測量作n次測量,表征測量結果分散性的量s,可用貝塞爾公式算出。稱s為單次測量的標準偏差,一般稱其為實驗標準偏差,是表征測量結果分散性的重要參數。式中x為n次測量的算術平均值,xi-x=νi是殘差,n-1為自由度。可以看出,計算實驗標準偏差的3個重要參數是算術平均值、殘差和自由度。而σ為總體標準偏差,s為實驗標準偏差, 為總體方差, 為實驗方差。
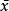 總體標準偏差
總體標準偏差當n→∞時, =μ,說明實驗標準偏差s與總體標準偏差σ的原始定義是一致的。而在n有限時,實驗標準偏差s計算所得的值只是總體標準偏差σ的一個估計值 。
意義
總體標準偏差σ的物理意義是:當一台確定的儀器對同一物理量進行n次重複測量時,表述該測量列隨機誤差的分散程度,σ越小。說明該儀器的精密度越好,反之精密度越差;或者,當用一台確定的儀器對一批 個(或n組)零件進行測量時,表達該組被測件隨機誤差的分散程度, σ越小,說明該批零件的工藝穩定性好,反之,工
藝穩定性差。
可以看出,通過測量誤差引出了算術平均值,通過算術平均值引出了殘差和自由度, 進而引出了實驗標準偏差,實驗標準偏差用來表征對同一被測量作n次測量結果的分散性。而表征合理地賦予被測量之值的分散性,並與測量結果相聯繫的參數就是測量不確定度。因此,實驗標準偏差是測量不確定度評定的重要參數,也是測量不確定度評定的理論基礎。
無論是總體標準偏差σ還是實驗標準偏差s,都不是一個具體的誤差。它的數值大小隻不過說明在一定條件下進行一系列測量時, 隨機誤差出現的機率密度分布情況。σ值小表明測量值比較集中,σ值大表明測量值比較分散。所以,在測量中,取測量列的算術平均值作為測量結果,用實驗標準偏差表征測量值的分散程度。因此,算術平均值和實驗標準偏差是測量不確定度評定的數字特徵。
在實踐中的套用
用於測試儀器設備的精密度的評定
在編制儀器的檢定規程時,除通過一定的分析計算,最終還須進行一系列的實驗測試。用n次測試結果計算出 σ值,然後根據需要給定其極限誤差。如我廠自製一台稱重量用的測力裝置。被測參數為2000kg士15% 。該裝置的允許極限誤差究竟給多大才合理,保證使用要求?我們用三等測力計對其進行20次等精度測量。算出 σ=4.54,我們取極限誤差為3σ=15kg,證明該裝置能滿足使用要求。
用於工藝穩定性的評定
當儀器不變,被測對象改變,即用同一台儀器對同一批零件進行n件(或n組)測量,根據測量結果計算出 σ,以便進行工藝調整,尤其對特殊精密加工設備大修後的考核。除按規程經機修檢驗外,一般都要試加工零件。送計量室,給出結論。這裡就不能以一兩件零件來評定,而應重複加工數件,用確定修後結果。
精度檢定
當被測零件(或參數)精度特別高,又無更高精度的儀器可供選擇,而在已有的幾台同類儀器上分別測量時。其結果差異又較大(儀器均合格),則可對幾台儀器進行等精度檢定,分別計算出各自的σ值。在別無選擇的情況下,即可選其中σ最小的一台用於該零件的測量。
用於測量爭議的間接仲裁
當對一批測量值供需雙方有爭議,又不便對提出異議方的實物進行複測時,則可從被訴方同一批尚存的樣件中抽取n個子樣進行複測(或從原記錄中抽取n個數值)計算出σ值(為慎重,可同時覆核一下計量器具的合格性),再根據對方提供的數據算出σ1值。如果被訴方的計量器具合格,且選擇符合誤差要求,當出現 σ1>>σ 時,即可斷定σ1方的測量不準。利用這種分析方法可避免盲目退貨或盲目派員處理。如寶鋼就曾用此方法處理一起涉外爭議:一批出口鋼坯,對方提出異議,他們在確認計量器具合格的基礎上,從未發出的同一批中抽取32件進行複測,算出σ=0.03,據對方提供的數據算出σ1=0.21,σ1>> σ,因此確認對方測量有誤。對方終於接受了寶鋼的結論,撤銷了異議 。