二進制數編碼
 編碼方法
編碼方法 編碼方法
編碼方法 編碼方法
編碼方法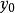 編碼方法
編碼方法設真值 是一個包括1位符號位的n+1位整數真值(注意: 是符號位); 是一個包括1位符號位的n+1位小數真值(注意: 是符號位)。
顯然,x和y的數值部分均為n位。據此,給出二進制數原碼、反碼、補碼、移碼的定義。
原碼
整數x和小數y的原碼分別定義為:
 編碼方法
編碼方法 編碼方法
編碼方法反碼
整數x和小數y的反碼分別定義為:
 編碼方法
編碼方法 編碼方法
編碼方法補碼
整數x和小數y的補碼分別定義為:
 編碼方法
編碼方法 編碼方法
編碼方法其中,當x補與x的位數相同時,使用第二個式子;當x補比x少1位時,使用第三個式子。
移碼
整數移碼定義為:
 編碼方法
編碼方法其中,當x移與x的位數相同時,使用第一個式子;當x移比x少1位時,使用第二個式子。
十進制編碼
 編碼方法
編碼方法 編碼方法
編碼方法 編碼方法
編碼方法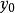 編碼方法
編碼方法設真值 是一個包括1位符號位的n+1位整數真值(注意: 是符號位); 是一個包括1位符號位的n+1位小數真值(注意: 是符號位)。即,x和y的數值部分均為n位。據此,給出十進制數原碼、反碼、補碼、移碼的定義。
十進制原碼
整數x和小數y的十進制原碼分別定義為:
 編碼方法
編碼方法 編碼方法
編碼方法十進制反碼
整數x和小數y的十進制反碼分別定義為:
 編碼方法
編碼方法 編碼方法
編碼方法十進制補碼
整數x和小數y的十進制補碼分別定義為:
 編碼方法
編碼方法 編碼方法
編碼方法其中,當x補與x的位數相同時,使用第二個式子;當x補比x少1位時,使用第三個式子。
補充說明
①當真值為正數時,原碼、反碼和補碼均為“符號-數值”碼,只要將真值的“+”號用“0”取代即可。
②當真值為負數時,原碼、反碼和補碼的數符和數值均由定義直接求出,但在求定義域端點之值時,有時要對結果加以簡單處理。其符號是二進制為“1”,十進制為“9”。
③當真值為二進制整數時,移碼才有定義移碼的數值部分與二進制整數補碼完全相同;符號則恰恰相反,即正數時為“1",負數時為“0"。
示例
已知二進制真值x=-0000,求其補碼。
解:x共5位:符號位為1位,數值位n為4,則:
 編碼方法
編碼方法x補=
 編碼方法
編碼方法補碼基於“同餘”概念,此處模為應丟掉,即最高位[1]應該丟掉,故其結果為00000。該數連同符號位一起共5位數,這就是上述提到的對定義域“端點”之值進行處理的問題。結果說明,在補碼系統中,0有唯一的表示,即+0=-0=0。

