基本介紹
香農編碼嚴格意義上來說不是最佳碼,它是採用信源符號的累計機率分布函式來分配碼字。
編碼步驟如下:
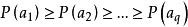 香農編碼
香農編碼(1)將信源符號按機率從大到小順序排列,為方便起見,令 ;
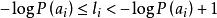 香農編碼
香農編碼(2)按 計算第i個符號對應的碼字的碼長(取整);
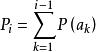 香農編碼
香農編碼(3) 計算第i個符號的累加機率 ;
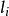 香農編碼
香農編碼(4)將累加機率變換成二進制小數,取小數點後 位數作為第i個符號的碼字。
香農編碼的效率不高,實用性不大,但對其他編碼方法有很好的理論指導意義。一般情況下,按照香農編碼方法編出來的碼,其平均碼長不是最短的。即不是緊緻碼(最佳碼)。只有當信源符號的機率分布使不等式左邊的等號成立時,編碼效率才達到最高 。
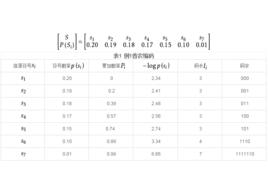
例1對如下信源編碼:
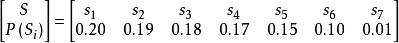 香農編碼
香農編碼 信源符號 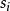 香農編碼 香農編碼 | 符號機率 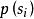 香農編碼 香農編碼 | 累加機率 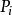 香農編碼 香農編碼 | 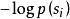 香農編碼 香農編碼 | 碼長 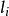 香農編碼 香農編碼 | 碼字 |
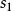 香農編碼 香農編碼 | 0.20 | 0 | 2.34 | 3 | 000 |
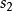 香農編碼 香農編碼 | 0.19 | 0.2 | 2.41 | 3 | 001 |
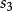 香農編碼 香農編碼 | 0.18 | 0.39 | 2.48 | 3 | 011 |
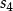 香農編碼 香農編碼 | 0.17 | 0.57 | 2.56 | 3 | 100 |
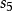 香農編碼 香農編碼 | 0.15 | 0.74 | 2.74 | 3 | 101 |
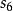 香農編碼 香農編碼 | 0.10 | 0.89 | 3.34 | 4 | 1110 |
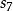 香農編碼 香農編碼 | 0.01 | 0.99 | 6.66 | 7 | 1111110 |
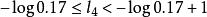 香農編碼
香農編碼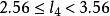 香農編碼
香農編碼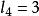 香農編碼
香農編碼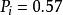 香農編碼
香農編碼其香農編碼如表1所示,以i=4為例, ,即 ,因此 。累加機率 ,變成二進制數,為0.1001...。轉換的方法為:用P乘以2,如果整數部分有進位,則小數點後第一位為1,否則為0,將其小數部分再做同樣的處理,得到小數點後的第二位,依此類推,直到得到了滿足要求的位數,或者沒有小數部分了為止。
可以看出,編碼所得的碼字,沒有相同的,所以是非奇異碼,也沒有一個碼字是其他碼字的前綴,所以是 即時碼,也是唯一可解碼。
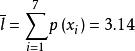 香農編碼
香農編碼平均碼長為: 碼符號/符號;
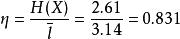 香農編碼
香農編碼平均信息傳輸效率為: 比特/碼符號。
香農編碼的效率不高,實用性不大,但對其他編碼方法有很好的理論指導意義。一般情況下,按照香農編碼方法編出來的碼,其平均碼長不是最短的,即不是緊緻碼(最佳碼)。只有當信源符號的機率分布使不等式左邊的等號成立時,編碼效率才達到最高。
最佳碼
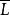 香農編碼
香農編碼 香農編碼
香農編碼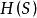 香農編碼
香農編碼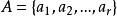 香農編碼
香農編碼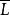 香農編碼
香農編碼最佳碼(optimal code)是信源編碼的一種類型,對於某一信源和某一碼元集,若有一個惟一可解碼,其平均長度 小於等於所有其他惟一可解碼的平均長度,則稱該碼為 最佳碼或 緊緻碼。無失真信源編碼的基本問題就是尋找最佳碼。若一個離散無記憶信源 具有熵為 、並有碼元集 ,則總可找到一種無失真編碼方法,構成惟一可解碼,使其平均碼長 滿足
 香農編碼
香農編碼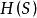 香農編碼
香農編碼上式表示最佳碼的平均長度的下限值與信源熵 成正比。
相關介紹
Huffman編碼
基本介紹
1952年赫夫曼(D.A. Huffman)提出了一種構造最佳碼的方法,稱之為 Huffman碼。Huffman碼適用於多元獨立信源,對於多元獨立信源來說它是最佳碼。它充分利用了信源機率分布的特性進行編碼,是一種最佳的逐個符號的編碼方法 。
二元Huffman編碼
二元Huffman碼的編碼步驟如下:
 香農編碼
香農編碼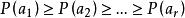 香農編碼
香農編碼1) 將 個信源符號按機率遞減的次序排列: 。
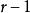 香農編碼
香農編碼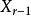 香農編碼
香農編碼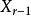 香農編碼
香農編碼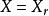 香農編碼
香農編碼2) 用0和1碼符號分別分配給機率最小的兩個信源符號,並將這兩個機率最小的信源符號合併成一個新符號,並用這兩個最小機率之和作為新符號的機率,從而得到由 個符號組成的新信源 ,稱 為信源 的縮減信源。
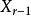 香農編碼
香農編碼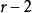 香農編碼
香農編碼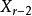 香農編碼
香農編碼3) 把縮減信源 的信源符號按機率遞減的次序排列,將其最後兩個機率最小的信源符號合併成一個新符號,並分別用0和1碼符號表示,形成 個符號的縮減信源 。
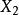 香農編碼
香農編碼4) 依次下去,直至縮減信源 只剩兩個符號為止。將最後兩個新符號分別用0和1碼符號表示(最後兩個符號的機率和為1)。然後從最後一級縮減信源開始,依編碼路徑由後向前返回,就得出各信源符號所對應的碼符號序列,即得對應的碼字。
Huffman編碼得到的碼並非是唯一的。這是因為以下兩點:
1) 每次對縮減信源最後兩個機率最小的符號分配0和1碼是可以任意的,所以可得到不同的編碼。
2) 若當縮減信源中縮減合併後的符號的機率與其他信源符號機率相同時,其不同的機率次序排列導致不同的編碼結果,但它們的平均碼長相同,方差不同。
通常,在Huffman編碼過程中,當縮減信源的機率分布重新排列時,應使合併得來的機率和儘量處於最高的位置,這樣可以使合併的元素重複編碼次數減少,使短碼得到充分利用。
特點
Huffman碼具有以下3個特點:
1) Huffman碼的編碼方法保證了機率大的符號對應短碼,機率小的符號對應長碼,而且短碼得到充分利用。
2) 每次縮減信源的最後兩個碼字總是最後一位碼元不同,前面各位碼元相同(二元編碼情況)。
3) 每次縮減信源的最長兩個碼字有相同的碼長。
這三個特點保證了所得的Huffman碼一定是最佳碼。
s元Huffman編碼
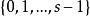 香農編碼
香農編碼上面討論的是二元Huffman碼,它的編碼方法同樣可以推廣到s元編碼中。不同的只是每次把s個符號(機率最小的)合併成一個新的信源符號,並分別用 等碼元。
為了充分利用短碼資源使平均碼長最短,必須使最後一步的縮減信源有s個信源符號。因此對於s元編碼,信源X的符號個數r必須滿足
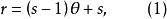 香農編碼
香農編碼 香農編碼
香農編碼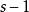 香農編碼
香農編碼式中, 表示縮減的次數; 為每次縮減所減少的信源符號個數。
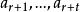 香農編碼
香農編碼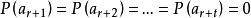 香農編碼
香農編碼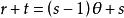 香農編碼
香農編碼若r不滿足式(1),可以增加t個信源符號 ,令其機率為零,即 ,滿足 。這樣得到的s元Huffman碼一定是最佳碼。
三元Huffman碼的性能不如二元Huffman碼的性能好。
Huffman碼的最佳性
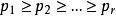 香農編碼
香農編碼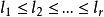 香農編碼
香農編碼不失一般性,可以假設信源的機率分布按大小次序排列,即如 ,其對應的碼長分別為 。
定理1對於給定分布的任何信源,存在一個最佳二元即時碼(其平均碼長最短),此碼滿足以下性質:
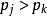 香農編碼
香農編碼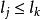 香農編碼
香農編碼1) 若 ,則 。
2) 兩個最小機率的信源符號所對應的碼字具有相同的碼長。
3) 兩個最小機率的信源符號所對應的碼字,除最後一位碼元不同外,前面各位碼元都相同。
 香農編碼
香農編碼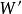 香農編碼
香農編碼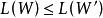 香農編碼
香農編碼定理2二元Huffman碼一定是最佳即時碼。即若 是Huffman碼, 是任意其他即時碼,則有 。
Fano編碼
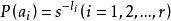 香農編碼
香農編碼1949年費諾(R.M. Fano)提出了一種編碼方法,稱之為Fano碼。它屬於機率匹配編碼,但 一般也不是最佳的編碼方法,只有當信源的機率分布呈現 分布形式的條件下,才能達到最佳碼的性能。
Fano碼的編碼步驟如下:
 香農編碼
香農編碼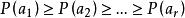 香農編碼
香農編碼1)將 個信源符號按機率遞減的方式進行排列: 。
2)將排列好的信源符號按機率值劃分成兩大組,使每組的機率之和接近於相等,並對每組各賦予一個二元碼符號0和1。
3)將每一大組的信源符號再分成兩組,使劃分後的兩個組的機率之和接近於相等,再分別賦予一個二元碼符號0和1。
4)依次下去,直至每個小組只剩一個信源符號為止。
5)將逐次分組過程中得到的碼元排列起來就是各信源符號的編碼。
Fano碼具有以下性質:
1)Fano碼的編碼方法實際上是一種構造碼樹的方法,所以Fano碼是即時碼。
2)Fano碼考慮了信源的統計特性,使機率大的信源符號能對應碼長較短的碼字,從而有效地提高了編碼效率。
3) Fano碼不一定是最佳碼。因為Fano編碼方法不一定能使短碼得到充分利用。當信源符號較多時,若有一些符號機率分布很接近,分兩大組的組合方法就會很多。可能某種分大組的結果,會使後面小組的“機率和”相差較遠,從而使平均碼長增加。
前面討論的Fano碼是二元Fano碼,對於s元Fano碼,與二元Fano碼的編碼方法相同,只是每次分組時應將符號分成機率分布接近的s個組 。
一般Fano編碼的平均碼長的界限為
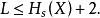 香農編碼
香農編碼