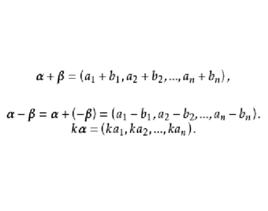矩陣的線性運算
矩陣的加法和數乘運算,統稱為矩陣的 線性運算。
矩陣加減法
定義 設
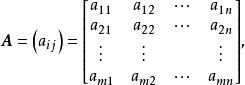 線性運算
線性運算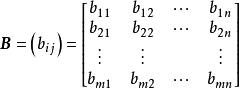 線性運算
線性運算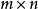 線性運算
線性運算是兩個 型矩陣,則矩陣
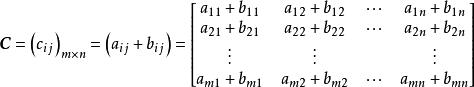 線性運算
線性運算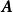 線性運算
線性運算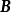 線性運算
線性運算稱為 和 的和,記為
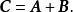 線性運算
線性運算矩陣的加法就是矩陣對應元素相加,當然,相加的矩陣必須要有相同的行數和列數,即只有同型矩陣方可相加。
由於矩陣加法歸結為它們元素的加法,即數的加法,故不難驗證矩陣加法滿足:
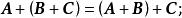 線性運算
線性運算(1)結合律:
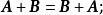 線性運算
線性運算(2)交換律:
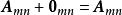 線性運算
線性運算明顯地,對零矩陣,有 。
定義2 矩陣
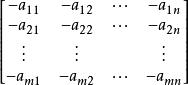 線性運算
線性運算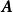 線性運算
線性運算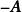 線性運算
線性運算稱為矩陣 的負矩陣,記為。
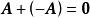 線性運算
線性運算顯然,有 一0,從而可定義矩陣減法為
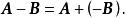 線性運算
線性運算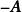 線性運算
線性運算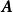 線性運算
線性運算我們可以將負矩陣 看做是實數一1和矩陣 相乘所得,從而抽象出一般數和矩陣的數量乘法。
矩陣數量乘積
定義 矩陣
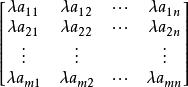 線性運算
線性運算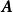 線性運算
線性運算 線性運算
線性運算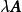 線性運算
線性運算 線性運算
線性運算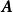 線性運算
線性運算 線性運算
線性運算稱為矩陣 與數 的數量乘積,記為。換句話說,用數 乘以矩陣 ,就是把矩陣的每個元素都乘上 。
不難驗證。數量乘積滿足下列運算規律:
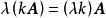 線性運算
線性運算(1) (結合律);
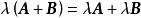 線性運算
線性運算(2) ;
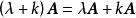 線性運算
線性運算(3) 。
向量的線性運算
向量的加法和數乘運算,統稱為 向量的線性運算。
向量的加減法
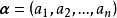 線性運算
線性運算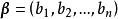 線性運算
線性運算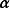 線性運算
線性運算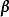 線性運算
線性運算設n維向量 , ,規定向量 與 的和為
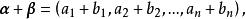 線性運算
線性運算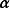 線性運算
線性運算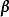 線性運算
線性運算規定向量 與 的差為
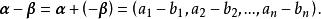 線性運算
線性運算向量的數乘
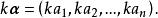 線性運算
線性運算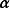 線性運算
線性運算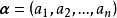 線性運算
線性運算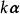 線性運算
線性運算設n維向量 ,各分量乘以數k所構成的向量,稱為數k與向量的數量乘積,簡稱數乘,記做 ,即
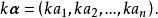 線性運算
線性運算容易驗證得到:
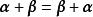 線性運算
線性運算(1 ) (加法交換律);
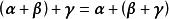 線性運算
線性運算(2) (加法結合律);
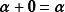 線性運算
線性運算(3) ;
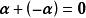 線性運算
線性運算(4) ;
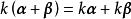 線性運算
線性運算(5) (數乘分配律);
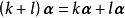 線性運算
線性運算(6) (數乘分配律);
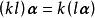 線性運算
線性運算(7) (數乘結合律);
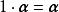 線性運算
線性運算(8) 。
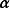 線性運算
線性運算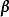 線性運算
線性運算上述定義與性質是針對行向量而言的,當與為列向量時,有類似結論。