定義
如下線性時滯系統：
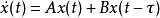線性時滯系統
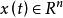線性時滯系統
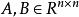線性時滯系統式中， ， ， τ ≥0為時滯。
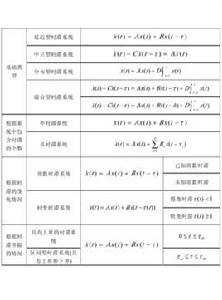
線性時滯系統的分類
通常，將線性時滯系統分為以下三種類型。
（1）第一類是延遲型時滯系統 ：
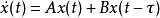線性時滯系統該系統中的時滯τ 存在於系統的狀態變數中，這樣的時滯τ 稱為離散時滯。
（2）第二類是中立型時滯系統：
圖1 線性時滯系統分類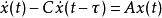
線性時滯系統該系統中的時滯τ 存在於系統狀態變數的導數中，這樣的時滯τ 稱為中立時滯。
（3）第三類是分布型時滯系統：
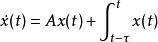線性時滯系統該系統中的時滯作用為過去一段時間系統變數的積分，這樣的時滯稱為分布時滯。
有時候，一個系統中可能同時含有以上兩種或三種類型的時滯：
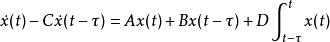線性時滯系統而且三種類型的時滯也可以是不同的：
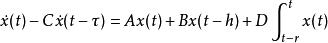線性時滯系統線性時滯系統根據其中時滯的個數以及變化情況等各種因素，可以分為很多類型，如圖1所示。
線性時滯系統穩定性分析方法
線性時滯系統的穩定性分析方法可分成 3 類。
無限維系統理論方法
這種方法是將時滯系統看成無窮維系統，用無窮維空間的適當運算元來描述時滯系統的狀態變化，一方面可對時滯系統進行一般建模；另一方面，也可表述系統的可觀性和可控性等結構方面的概念。
代數系統理論方法
代數系統理論對於時滯系統的建模和分析都比較方便，但在控制器的設計方面目前尚處於初期階段，還缺乏有效方法。
泛函微分方程理論方法
泛函微分方程理論考慮了系統的過去對系統變化率的影響，利用有限維空間以及泛函空間提供一套適當的數學結構以描述時滯系統的狀態變化。研究時滯系統主要是套用泛函微分方程理論，研究範圍涉及穩定性分析、控制器設計、控制、無源與耗散控制、可靠控制、保成本控制、濾波、Kalman 濾波以及隨機控制等。不管研究哪個分支， 穩定性都是基礎，對最終形成控制方案具有非常重要的理論和現實意義。 時滯系統穩定性分析的目的是希望找到計算簡單、切實有效並且保守性儘可能小的穩定性判據。研究方法主要分為兩類： 一類是以研究系統傳遞函式為主的頻域方法；另一類是以研究系統狀態方程為主的時域( 狀態空間) 方法。
研究方法
關於時滯系統穩定性的研究，兩種主要的研究方法為頻域方法和時域方法。
頻域法
頻域法用經典控制理論的分析方法通過分析系統特徵根的分布來判斷時滯系統的穩定性。例如考慮如下系統：
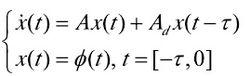線性時滯系統 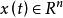線性時滯系統
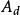線性時滯系統其中，是系統的狀態向量， A 和是具有適當維數的已知實常數矩陣，τ ≥ 0是時滯， φ (t)是初始條件。
上述系統穩定的充分必要條件是系統的特徵方程
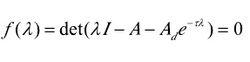線性時滯系統的根均具有負實部。但時滯系統是無窮維系統，特徵方程有無窮多個特徵根，計算所有的特徵根是不現實的，而且也沒有實際意義。
基於頻域的分析方法直觀，容易理解，但是其缺點是不能處理時變和參數攝動的不確定性，用頻域法研究時滯系統的穩定性具有較強的局限性。
時域法
時域法簡單易算、容易與現代代數和幾何等數學工具相結合進行時滯系統的分析，並且能夠對時變時滯系統以及具有系統矩陣的參數不確定性、外界干擾不確定和時滯本身不確定性等的不確定時滯系統進行穩定性分析以及控制器綜合。
時域法主要是運用 Lyapunov 穩定性理論得到的 Lyapunov-Krasovskii 穩定性定理和 Razumikhin 穩定性定理來進行時滯系統的穩定性分析。總體來說，Lyapunov-Krasovskii 泛函方法要比 Lyapunov-Razumikhin 函式方法保守性更低，近年來，基於 Lyapunov-Krasovskii 泛函方法的穩定性結果占據了時滯系統穩定性分析和綜合的主要部分。
