基本概念
線性系統是指同時滿足疊加性與均勻性(又稱為其次性)的系統。所謂疊加性是指當幾個輸入信號共同作用於系統時,總的輸出等於每個輸入單獨作用時產生的輸出之和;均勻性是指當輸入信號增大若干倍時,輸出也相應增大同樣的倍數。
時變系統(time-varying system)其中一或一個以上的參數值隨時間而變化,從而整個特性也隨時間而變化的系統。時變系統的特點是,其輸出回響的波形不僅同輸入波形有關,而且也同輸入信號加入的時刻有關。
線性時變系統即同時滿足線性系統和時變系統特徵的系統,它滿足系統疊加性與均勻性的特點,同時,當系統中某個參數值隨時間而變化時,整個特性也隨時間而變化。
表示
狀態方程
n維線性時變系統的狀態方程為:
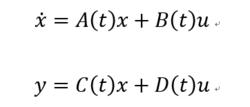 線性時變系統
線性時變系統其中,u是p維輸入向量,y是q維輸出向量。A、B、C、D分別是線性系統的參數,均是時間t的函式,即參數隨時間的變化 變化。
結構圖
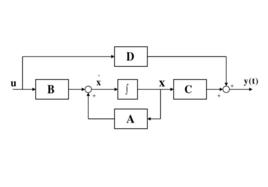
線性時變系統的結構圖如下:
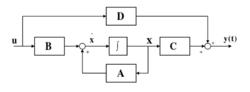 線性時變系統
線性時變系統能控性
對於線性時變系統,當t0時刻其x值為x0,在定義時間[t0,t1]時間內,狀態完全能控 的充要條件是Gram矩陣
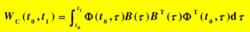 線性時變系統
線性時變系統非奇異。式中Φ(t,t0)為時變系統狀態轉移矩陣。
推論1(秩判據):
假設矩陣A(t)和B(t)都是n-1此連續可微的,在時間區間[t0,t1]上,若有
 線性時變系統
線性時變系統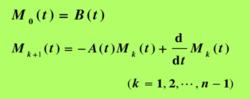 線性時變系統
線性時變系統則系統狀態完全能控,其中分塊矩陣
推論2(秩判據):
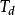 線性時變系統
線性時變系統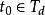 線性時變系統
線性時變系統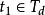 線性時變系統
線性時變系統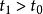 線性時變系統
線性時變系統假設矩陣A(t)和B(t)都是n-1此連續可微的,在時間區間 上是n-1次連續可微的,若對初始時刻 ,存在有限時刻 , ,使得
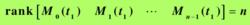 線性時變系統
線性時變系統則系統在時刻t0是狀態完全能控的,其中分塊矩陣
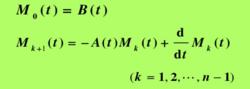 線性時變系統
線性時變系統能觀性
線性時變系統
 線性時變系統
線性時變系統在定義時間[t0,t1]時間內,狀態完全能觀的充要條件是Gram矩陣
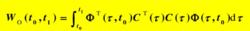 線性時變系統
線性時變系統為非奇異。
推論1(秩判據):
假設矩陣A(t)和C(t)都是n-1次連續可微的,在時間區間[t0,t1]上,又有
 線性時變系統
線性時變系統則系統是狀態完全能觀的,其中分塊矩陣
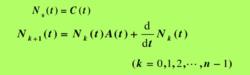 線性時變系統
線性時變系統推論2(秩判據):
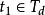 線性時變系統
線性時變系統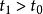 線性時變系統
線性時變系統對於連續時間線性時變系統,假設矩陣A(t)和C(t)都是n-1階連續可導的函式矩陣,則系統在時刻t0狀態完全能觀的充要條件為:在一個有限時刻 , ,使得
 線性時變系統
線性時變系統則系統是狀態完全能觀的,其中分塊矩陣
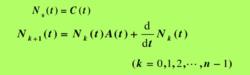 線性時變系統
線性時變系統穩定性
穩定性是設計控制系統的最基本要求 。
線性時變系統方程:
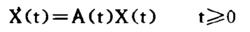 線性時變系統
線性時變系統如果已經求出矩陣A(t)的所有特徵值,系統漸近穩定的充要條件是:A(t)的所的特徵值都位於S的左半平面。