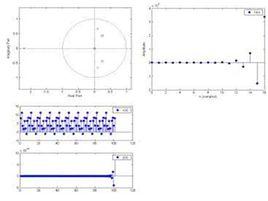
簡介
從系統理論的觀點看，任何實際系統的過去狀態不可避免地要對當前的狀態產生影響，即系統的演化趨勢不僅依賴於系統當前的狀態，也依賴於過去某一時刻或若干時刻的狀態，這類系統稱為時變時滯系統。時變時滯產生的原因有很多，如：系統變數的測量(複雜的線上分析儀)、長管道進料或皮帶傳輸、緩慢的化學反應過程等都會產生時變時滯。時變時滯常見於電路、光學、神經網路、生物環境及醫學、建築結構、機械等領域，由於套用背景廣泛，受到很多學者的關注。從理論分析的角度來看，在連續域中，時變時滯系統是一個無窮維的系統，特徵方程是超越方程，有無窮多個特徵根。而在離散域中，時變時滯系統的維數隨時滯的增加按幾何規律增長，這給系統的穩定性分析和控制器設計帶來了很大的困難 。
特點
時變時滯系統的特點是，其輸出回響的波形不僅同輸入波形有關，而且也同輸入信號加入的時刻有關。這一特點增加了分析和研究的複雜性。對於時變時滯系統來說，即使系統是線性的，也只能採用時間域的描述。描述的基本形式是變係數的微分方程或差分方程。時變時滯系統的運動分析比定常系統要複雜得多。在工程中，套用最廣的是所謂凍結係數法，這一方法的實質是在系統工作時間內，分段將時變參數“凍結”為常值，從而可分段地把系統看成為定常系統進行研究。通常，凍結參數法只對參數變化比較緩慢的時變時滯系統才有效。對時變時滯系統控制的一個可能的方案是，在採用估計器對參數進行線上估計的同時，採用適應控制系統實現控制 。
表示
n維線性時變時滯系統的狀態方程為：
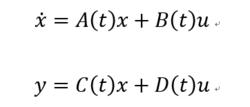時變時滯系統其中，u是p維輸入向量，y是q維輸出向量。A、B、C、D分別是線性系統的參數，均是時間t的函式，即參數隨時間的變化而變化。
線性時變時滯系統的結構圖如下：
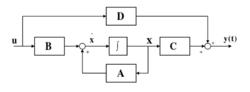時變時滯系統穩定性
穩定性是設計控制系統的最基本要求。
線性時變時滯系統方程：
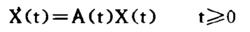時變時滯系統如果已經求出矩陣A(t)的所有特徵值，系統漸近穩定的充要條件是：A(t)的所的特徵值都位於S的左半平面。
展望
由於時變時滯系統本身的複雜性，以及時變時滯特性的多元性和疊加性，致使這一研究領域中仍有大量的空白和難題沒有涉及和解決。結合目前該領域的研究現，理論方法需要進一步完善的有：
1、“快”時變問題。針對更為一般的快時變時滯系統(如高階線性快時變時滯系統、非線性快時變時滯系統等)，如何放寬現有方法對時變時間的要求，套用這些控制策略及算法進行實時的系統辨識與控制，或在此基礎上作進一步的改進與更新等，尚有待更全面深入的研究。
2、系統的條件穩定問題。一般情況下，控制算法對於某一類時變系統而言都需要附加或多或少的穩定性條件或假設。針對此類問題，如何能夠使這些為了保證系統穩定而提出的條件或假設不影響系統性能、產生儘可能少的限制。是將控制算法套用到實際控制過程的關鍵，因而具有非常重要的研究意義。
3、實時建模問題。建模的精確性與快速性通常對控制系統的性能具有直接影響，同時也關係到控制方法的可操作性。因此，若能夠在時變系統的實時建模問題上進行深入研究，必將有利於時變系統控制方法的進一步套用與發展。
4、非線性問題。在非線性情況下，時變系統的微分方程的解析解往往不存在，甚至時變模型也不可得。如何利用現有的線性模型與時變系統控制方法。將其進一步推廣至非線性系統，或者如何將非線性時變系統分段線性化，找出可與某些線性特性相替換的非線性特性，值得進行更加深入的討論。
另一方面，從實際套用的角度,有以下幾個問題需作進一步的探討：
1、數據處理問題。對於實際過程中的動態數據需要進行適當的信號處理與分析，突出數據中的系統性信息，降低不相關的干擾噪聲，在能夠表徵實際系統時變特性的基礎上儘量降低系統複雜。
2、適用條件問題。在將理論方案付諸實踐時，需要事先對實際的時變對象作出準確判斷，根據具體情況選擇適用的解決方案，必要時還要對理論方法作些靈活的調整甚至改進。
3、時變因素的不確定問題。由於實際系統往往複雜多變,存在大量的不確定因素，為節省研究成本並提高工作效率，可以採取仿真實驗與實際相結合的方法，必要時甚至需要設定多種控制方案。同時對實際系統的時變環境也要有足夠的了解，在仿真實驗時需對控制方法進行儘可能全面的可行性討論，在實際套用時再進行準確快速的調整。
