定義
定義1 設x，x，…，x是線性空間E的有限個向量，x∈E，如果存在數c，c，…，c使得
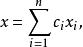線性表示則稱x可由x，x，…，x 線性表示，或x是x，x，…，x的 線性組合。
舉例
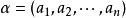線性表示例1 任意一個n維向量都是向量組
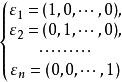線性表示的一個線性組合。因為
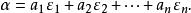線性表示例2 由定義1可以立即看出，零向量是任一向量組的線性組合（只要取係數全為0就可以了）。
相關概念
等價向量組
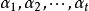線性表示
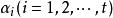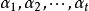線性表示
線性表示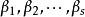 線性表示 線性表示定義2 如果向量組中每一個向量都可以由向量組線性表示，那么向量組就稱為可由向量組線性表示。如何兩個向量組互相可以線性表示，它們就稱為 等價。
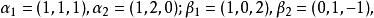線性表示
線性表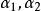示
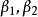線性表示例如，設則向量組與向量組是等價的。
註：向量組之間的等價滿足反身性、對稱性和傳遞性。
線性相關
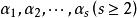線性表示
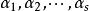線性表示定義3 如果向量組中有一個向量可以由其餘的向量線性表示，那么向量組稱為 線性相關的。
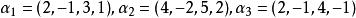線性表示例如，向量組是線性相關的，因為
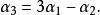線性表示註：由定義3可知，任意一個包含零向量的向量組一定是線性相關的。
重要性質
向量組B=(β，β，……，β)能由向量組A=(α，α，……，α)線性表示的充要條件是矩陣A=(α，α，……，α)的秩等於矩陣(α，α，……，αB)的秩。
1.B=(β，β，……，β)
2.向量組 B能由向量組 A線性表示，則向量組 B的秩不大於向量 A的秩。反之不一定成立。
3.① 一個向量可由向量組中其餘向量線性表示，前提是這個向量組線性相關。
②線性相關的向量組中並不是任一向量都可由其餘向量線性表示；但當其餘向量線性無關時，這個向量必可由其餘向量線性表示。
4.零向量可由任一組向量線性表示。
5.向量組 α，α，……，α 中每個向量都可由向量組本身線性表示。
6.任一 n維向量 α =（α，α，……，α）都可由 n維單位向量組線性表示。
7.設 α，α，……，α線性無關 ，而 α，α，……，αß線性相關，則 β可由 α，α，……，α線性表示 ，且表示是唯一的。
