圖像表示
正文
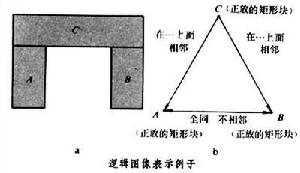
圖像信息在計算機中的表示和存儲方式。圖像表示和圖像運算一起組成圖像模型，是模式分析中的重要組成部分。可以在圖像信息的不同等級上對圖像進行表示。最基本的物理圖像是根據矩形格線抽樣原理從連續圖像域中抽取二維灰度陣列（矩陣）得到的。也可以用長向量表示二維灰度矩陣，它是按列（或行）掃描灰度矩陣，把下一列（或行）的頭和前一列（或行）的尾相接而成。它們的線性可逆變換同樣可以用來表示圖像。圖像的每一行由行程（具有同一灰度的鄰近像元集合）序列所組成，因此也可以用行程長度編碼（見圖像編碼）表示圖像。另一種表示圖像的方法是四分樹，它是用樹的根節點表示整個圖像：假使圖像的灰度都取同一數值，就把根節點標上該灰度，並停止產生後繼節點，否則就對根節點加入四個後繼節點，每個後繼點表示圖像的一個象限。假使其中的某個象限有同一灰度，就把和它對應的節點標上該灰度，並停止產生該節點的後繼節點，否則重複上述產生四個後繼節點的過程，直到所有的節點所對應的區域灰度都相同為止。假使圖像的大小是2k×2k，若把根節點作為0級節點，則第k級節點就和一個像素相對應。這種表示方法能夠減少存儲量而且有相應的算法進行圖像的基本運算，如鄰域查找等。其缺點是圖像的相對位移會使四分樹表示發生改變，從而很難從四分樹表示判斷兩幅圖像是否全同。另一種圖像表示方法是在抽取對象的邊界或區域的基礎上，對邊界或區域進行描述，例如從邊界上任意點出發沿邊界進行跟蹤，用數字表示跟蹤方向，從而得到邊界的數字鏈碼錶示。也可以用形狀分析的方法表示對象的區域（見圖像分割）。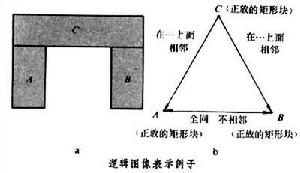
更高一級的圖像表示是描述圖像中的物體和物體間的關係。這樣一種圖像常常稱為邏輯圖像。圖像中的物體或組成部分可以用區域或一組幾何特性來表征，還可以詳細說明組成部分的位置和其他非幾何的屬性。一般用圖表示邏輯圖像，圖中節點表示物體的組成部分，每個節點用組成部分的有關性質作成的表作為標籤，必要時還可以用指針指向低一級水平的圖像數據結構（如形成該區域的灰度陣列數據）。節點之間的有向弧用來表示相應組成部分之間的關係，用關係性質作成的表作為弧的標籤。例如,圖b給出由三個矩形塊所組成的圖像（圖a）的邏輯圖像表示。此外，也可以用文法形式表示物體之間的關係（見模式文法）。 為了使各種表示在同一系統中同時存在，就需要有相應的算法把一種表示轉換為另一種表示，例如把二維陣列變換為四分樹,或從四分樹表示變換為二維陣列,以及從物理圖像轉換為邏輯圖像，或者如計算機作圖那樣從邏輯圖像數據得到相應的物理圖像數據。此外還應有修改數據（如在樹結構中增加或刪除一個節點）的程式方法。
三維圖像的一種表示方法是把三維陣列看成是由一系列二維圖像陣列所組成，從而可以套用二維圖像的表示方法；也可以類似四分樹的方法，把立方塊分解為原邊長的二分之一的八個小立方塊，遞歸地用八分樹表示三維圖像。另一種三維物體的近似表示方法是用廣義錐，所謂廣義錐是一個由軸、橫截面形狀和尺寸函數所組成的三元組。例如一個圓盤形以與軸成90°方向運動，且軸是一個水平線段並通過圓盤的中心，而尺寸函式又是一個常數時，就得到一個平放的圓柱體。任何複雜的三維物體都可以用相應的橫截面形狀沿軸線運動且尺寸大小按照尺寸函式改變所掃出的物體圖像來近似地表示。此外，三維物體的邊界可以用一組表面表示，其中每個表面可以用表面的斜率表征，從而可以用三維鏈碼錶示空間曲面。現代已研究出在二維圖像基礎上表示三維圖像信息的各種方法。
參考書目
A.Rosenfeld and A.C.Kak，Digital Picture Processing, Academic Press, New York,1982.
K.S.Fuand T.L.Kunii（editors），Picture Engineering， Springer-Verlag, Berlin, 1976.
