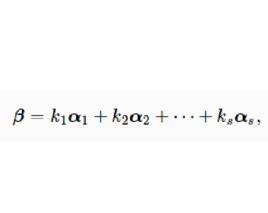定義
若干個同維數的行向量(或同維數的列向量)所組成的集合叫做 向量組。
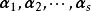 線性表出
線性表出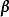 線性表出
線性表出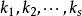 線性表出
線性表出對n維向量 和 ,如果存在實數 ,使得
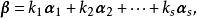 線性表出
線性表出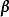 線性表出
線性表出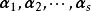 線性表出
線性表出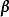 線性表出
線性表出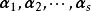 線性表出
線性表出稱向量 是向量 的 線性組合,或者說向量 可由 線性表出(示)。
 線性表出
線性表出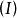 線性表出
線性表出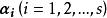 線性表出
線性表出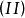 線性表出
線性表出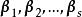 線性表出
線性表出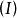 線性表出
線性表出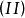 線性表出
線性表出設有兩個n維向量組 ;如果 中每個向量 都可由 中的向量 線性表出,則稱向量組 可由向量組 線性表出。
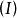 線性表出
線性表出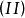 線性表出
線性表出如果 、 這兩個向量組可以互相線性表出,則稱這兩個 向量組等價。
註:(1)等價向量組具有傳逆性、對稱性、反身性;
(2)向量組和它的極大線性無關組是等價向量組;
(3)向量組的任意兩個極大線性無關組是等價向量組;
(4)等價的向量組有相同的秩。但秩相等的向量組不一定等價。
例題解析
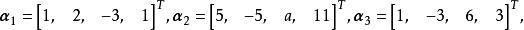 線性表出
線性表出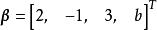 線性表出
線性表出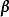 線性表出
線性表出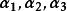 線性表出
線性表出例1 已知 ,試問當a,b取何值時 可以由 線性表示,並寫出其表達式。
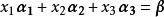 線性表出
線性表出解: 設 ,按分量寫出,即有
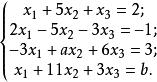 線性表出
線性表出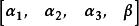 線性表出
線性表出對增廣矩陣 作初等行變換,有
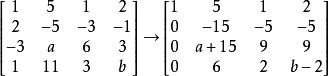 線性表出
線性表出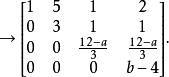 線性表出
線性表出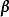 線性表出
線性表出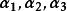 線性表出
線性表出如果b≠4,方程組無解, 不能由 線性表出。
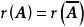 線性表出
線性表出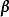 線性表出
線性表出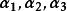 線性表出
線性表出如果b=4,秩 方程組有解, 可由 線性表出。
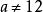 線性表出
線性表出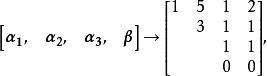 線性表出
線性表出(1)當 時,
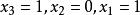 線性表出
線性表出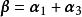 線性表出
線性表出方程組有唯一解: ,即。
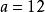 線性表出
線性表出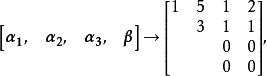 線性表出
線性表出(2)當 時,
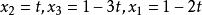 線性表出
線性表出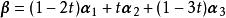 線性表出
線性表出方程組有無窮多解: ,即,t為任意實數。
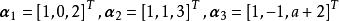 線性表出
線性表出例2 設有向量組(1): ;
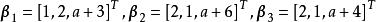 線性表出
線性表出(2): 。
試問:當a為何值時,向量組(1)與(2)等價?當a為何值時,向量組(1)與(2)不等價?
分析: 所謂向量組(1)與(2)等價,即向量組(1)與(2)可以互相線性表出,如果方程組
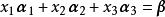 線性表出
線性表出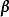 線性表出
線性表出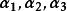 線性表出
線性表出有解,則 可以由 線性表出。
那么,如果對同一個a,三個方程組
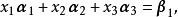 線性表出
線性表出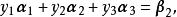 線性表出
線性表出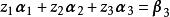 線性表出
線性表出均有解,則說明向量組(2)可以由向量組(1)線性表出
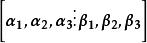 線性表出
線性表出解: 對 作初等行變換,有
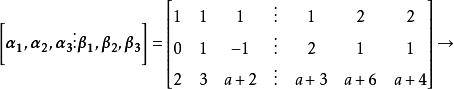 線性表出
線性表出 線性表出
線性表出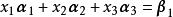 線性表出
線性表出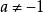 線性表出
線性表出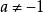 線性表出
線性表出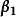 線性表出
線性表出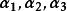 線性表出
線性表出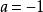 線性表出
線性表出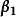 線性表出
線性表出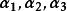 線性表出
線性表出那么,由方程組 知,只要方程組總有唯一解,即時,必可由線性表出,而時,方程組無解,不能由線性表出。
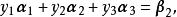 線性表出
線性表出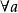 線性表出
線性表出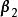 線性表出
線性表出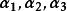 線性表出
線性表出由方程組知,方程組總有解,即必可由線性表出。
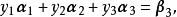 線性表出
線性表出 線性表出
線性表出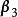 線性表出
線性表出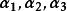 線性表出
線性表出由方程組知,只要,方程組就有解,就可由線性表出,
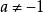 線性表出
線性表出因此,當時,向量組(2)可由向量組(1)線性表出。
反之,由於行列式
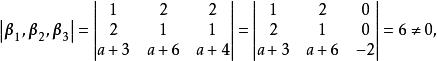 線性表出
線性表出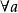 線性表出
線性表出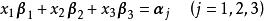 線性表出
線性表出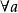 線性表出
線性表出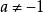 線性表出
線性表出故,三個方程組恆有解,即,向量組(1)總可由向量組(2)線性表出,因此,時向量組(1)與(2)等價。
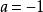 線性表出
線性表出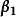 線性表出
線性表出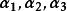 線性表出
線性表出而時,不能由線性表出,向量組(1)與(2)不等價。
評註: 若未知向量的坐標而要判斷能否線性表出的問題,通常是轉換為非齊次線性方程組是否有解的討論,如果向量的坐標沒有給出而問能否線性表出,通常用線性相關及秩的理論分析、推理。