簡介
線性非時變系統必須同時滿足線性和非時變性:
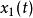 線性時不變系統理論
線性時不變系統理論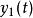 線性時不變系統理論
線性時不變系統理論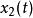 線性時不變系統理論
線性時不變系統理論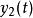 線性時不變系統理論
線性時不變系統理論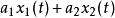 線性時不變系統理論
線性時不變系統理論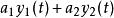 線性時不變系統理論
線性時不變系統理論 線性時不變系統理論
線性時不變系統理論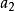 線性時不變系統理論
線性時不變系統理論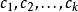 線性時不變系統理論
線性時不變系統理論線性,指系統的輸入和輸出之間的關係是一個線性映射:如果輸入產生回響,而輸入產生回響,那么放縮和加和輸入產生放縮、加和的回響,其中和為實標量。此性質可以拓展到任意項,於是對於實數,輸入
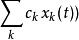 線性時不變系統理論
線性時不變系統理論產生輸出
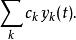 線性時不變系統理論
線性時不變系統理論特別地,輸入
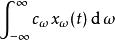 線性時不變系統理論
線性時不變系統理論產生輸出
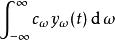 線性時不變系統理論
線性時不變系統理論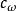 線性時不變系統理論
線性時不變系統理論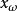 線性時不變系統理論
線性時不變系統理論 線性時不變系統理論
線性時不變系統理論其中,和是標量,而輸入在序號為 的連續統內變化。因此,如果輸入函式可以由一個連續統的輸入函式像上面展示的那樣,“線性”組合而成,則對應的輸出函式,可以通過相應連續統的輸出函式以相同的方式縮放和求和得到 。
 線性時不變系統理論
線性時不變系統理論 線性時不變系統理論
線性時不變系統理論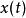 線性時不變系統理論
線性時不變系統理論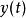 線性時不變系統理論
線性時不變系統理論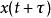 線性時不變系統理論
線性時不變系統理論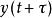 線性時不變系統理論
線性時不變系統理論時不變性,指如果將系統的輸入信號延遲秒,那么得到的輸出除了這秒延時以外是完全相同的,稱這樣的系統是“時不變”的。即若系統輸入,對應的輸出為,則輸入為時系統的輸出為。
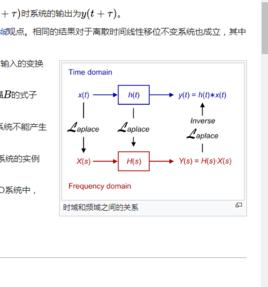
LTI系統的理論的基本結論是任何LTI系統都可以完全用一個單一方程來表示,稱為系統的衝激回響。系統的輸出可以簡單表示為輸入信號與系統的衝激回響的卷積。這種分析方法通常稱為時域觀點。相同的結果對於離散時間線性移位不變系統也成立,其中信號為離散時間取樣信號,並且卷積對序列定義。
同理,任何LTI系統的特徵可由頻域的系統傳遞函式刻畫,它是系統衝激回響的拉普拉斯變換(在離散時間系統的情況下為Z變換)。由於這些變換的性質,該系統在頻域的輸出是傳遞函式與輸入的變換的乘積。換句話說,時域中的卷積相當於頻域中的乘法。
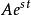 線性時不變系統理論
線性時不變系統理論 線性時不變系統理論
線性時不變系統理論 線性時不變系統理論
線性時不變系統理論 線性時不變系統理論
線性時不變系統理論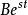 線性時不變系統理論
線性時不變系統理論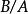 線性時不變系統理論
線性時不變系統理論 線性時不變系統理論
線性時不變系統理論對於所有的LTI系統中,本徵函式和所用變換的基函式,是復指數函式。這即是說,如果一個系統的輸入是復波形,復振幅為,復頻率為,輸出將是輸入的復常數倍,表示為新復振幅的式子。比值是頻率的傳遞函式。
因為是正弦的復指數與復共軛頻率的總和,如果輸入到該系統是一個正弦波,則系統的輸出也將是一個正弦波,或許具有不同振幅和不同相位的,但總是與相同的頻率在達到穩定狀態。LTI系統不能產生頻率成分中沒有的輸入。
LTI系統理論善於描述了許多重要的系統。至少相對於時間變化的和/或非線性的情況下最LTI系統被認為是“容易”來分析。任何可以被模擬為常係數線性齊次微分方程系統是LTI系統。這類系統的實例是電路由電阻器S,電感s和電容器S(RLC電路)的。理想的彈簧 - 質量 - 阻尼系統也是LTI系統,並且在數學上是等效的RLC電路。
最LTI系統概念都是連續時間和離散時間(線性移位不變)的情況下相似。在圖像處理中,時間變數被替換為2空間變數,時間不變性的概念被替換為二維移不變性。當分析濾波器組s和MIMO系統中,常常是有用考慮的信號矢量。
線性系統不是時不變可以用其他方法來解決,如格林函式方法。同樣的方法時,必須使用問題的初始條件是不為空。
重要的系統特性
因果性和穩定性是描述系統的兩個重要性質。如果獨立變數是時間,那么因果性是必須的,但並不是所有系統的獨立變數都是時間。例如,一個處理靜止圖像的系統不需要具備因果性。非因果系統可以建立,並可以在許多情況下發揮作用。即使是非實數系統也可以構建,並且在很多場合也是非常有用的。
因果性
如果系統輸出只與當前以及過去的輸入有關,那么該系統就是因果系統。因果性的充分必要條件是
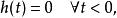 線性時不變系統理論
線性時不變系統理論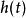 線性時不變系統理論
線性時不變系統理論其中是衝激回響。由於拉普拉斯變換的逆變換不確定,所以通常不能根據拉普拉斯變換確定系統的因果性。只有在確定了系統的收斂域之後才能確定該系統的因果性。
穩定性
如果系統對每個有界輸入來說輸出都是有界的,那么系統就是有界輸入有界輸出穩定的(BIBO穩定),用數學方法表示就是如果每個輸入滿足
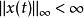 線性時不變系統理論
線性時不變系統理論就會導致輸出滿足
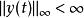 線性時不變系統理論
線性時不變系統理論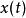 線性時不變系統理論
線性時不變系統理論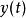 線性時不變系統理論
線性時不變系統理論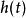 線性時不變系統理論
線性時不變系統理論(也就是說的最大絕對值是有界的意味著的最大絕對值也是有界的),那么系統就是穩定的。系統穩定的充分必要條件是衝激回響是在L1中(其L1範數有限)的:
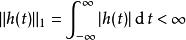 線性時不變系統理論
線性時不變系統理論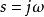 線性時不變系統理論
線性時不變系統理論在頻域中,收斂域必須包含虛軸。
 線性時不變系統理論
線性時不變系統理論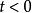 線性時不變系統理論
線性時不變系統理論作為一個例子,衝激回響等於Sinc函式的理想低通濾波器不是BIBO穩定的,因為Sinc函式不具有有限的L1範數。因此,對於一些有界輸入,理想低通濾波器的輸出是無界的。特別地,若對的輸入為零,並且在 時等於正弦信號的截止頻率,則在非過零時刻輸出是無界的。
衝激回響
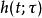 線性時不變系統理論
線性時不變系統理論在信號處理中,衝激回響(Impulse response)一般是指系統在輸入為單位衝激函式時的輸出(回響)。對於連續時間系統來說,衝激回響一般用函式來表示,相對應的輸入信號,也就是單位衝激函式滿足狄拉克δ函式的形式,其函式定義如下:
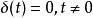 線性時不變系統理論
線性時不變系統理論並且,在從負無窮到正無窮區間內積分為1:
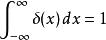 線性時不變系統理論
線性時不變系統理論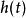 線性時不變系統理論
線性時不變系統理論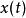 線性時不變系統理論
線性時不變系統理論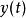 線性時不變系統理論
線性時不變系統理論在輸入為狄拉克δ函式時,系統的衝激回響包含了系統的所有信息。所以對於任意輸入信號,可以用連續域卷積的方法得出所對應的輸出。也就是:
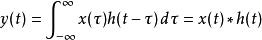 線性時不變系統理論
線性時不變系統理論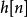 線性時不變系統理論
線性時不變系統理論對於離散時間系統來說,衝激回響一般用序列來表示,相對應的離散輸入信號,也就是單位脈衝函式滿足克羅內克δ的形式,在信號與系統科學中可以定義函式如下:
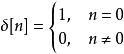 線性時不變系統理論
線性時不變系統理論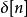 線性時不變系統理論
線性時不變系統理論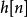 線性時不變系統理論
線性時不變系統理論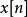 線性時不變系統理論
線性時不變系統理論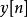 線性時不變系統理論
線性時不變系統理論同樣道理,在輸入為時,離散系統的衝激回響包含了系統的所有信息。所以對於任意輸入信號,可以用離散域卷積(求和)的方法得出所對應的輸出信號。也就是:
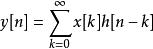 線性時不變系統理論
線性時不變系統理論