定義
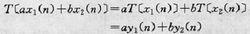圖1若y(n)及y(n)分別為某系統對輸入信號x(n)及x(n)的輸出回響，則該系統為線性系統的充分必要條件是如圖1。
其中a，b為任意常數，T為輸入至輸出的變換運算元。其物理概念可理解為：線性系統對兩個或兩個以上輸入信號的總回響等於該系統分別對其中各個輸入信號的回響之和（即疊加）。非移變特性是指在同樣起始狀態下系統的回響與輸入信號加於系統的位點（或時刻）無關。即如果系統對輸入信號：x(n)的回響是y(n)，則對x(n-k)的回響就是y(n-k)，其中k為整數，可正可負。若n代表時間，則顯然非移變性就相當於時間的移不變性。凡既滿足疊加性和齊次性又滿足非移變性的系統就是線性非移變系統，這一類系統的特性易於用數學表達，從而便於實現許多信號處理功能。又由於現實存在的各種系統中有許多種在一定的條件下均可近似於線性非移變系統，故長期以來對此類系統的研究一直受到廣泛的重視及套用。
線性系統的定義
線性系統是一數學模型，是指用線性運運算元組成的系統。相較於非線性系統，線性系統的特性比較簡單。線性系統需滿足線性的特性，若線性系統還滿足非時變性（即系統的輸入信號若延遲τ秒，那么得到的輸出除了這τ秒延時以外是完全相同的），則稱為線性時不變系統。
狀態變數和輸出變數對於所有可能的輸入變數和初始狀態都滿足疊加原理的系統。疊加原理是指:如果系統相應於任意兩種輸入和初始狀態(u1(t),x01)和(u2(t),x02)時的狀態和輸出分別為(x1(t),y1(t))和(x2(t),y2(t)), 則當輸入和初始狀態為(C1u1(t)+C2u2(t),C1x01+C2x02)時，系統的狀態和輸出必為(C1x1(t)+C2x2(t),C1y1(t)+C2y2(t)),其中x表示狀態,y表示輸出，u表示輸入，C1和C2為任意實數。一個由線性元部件所組成的系統必是線性系統。但是，相反的命題在某些情況下可能不成立。線性系統的狀態變數(或輸入變數)與輸出變數間的因果關係可用一組線性微分方程或差分方程來描述，這種方程稱為系統的數學模型。作為疊加性質的直接結果，線性系統的一個重要性質是系統的回響可以分解為兩個部分：零輸入回響和零狀態回響。前者指由非零初始狀態所引起的回響；後者則指由輸入引起的回響。兩者可分別計算。這一性質為線性系統的分析和研究帶來很大方便。
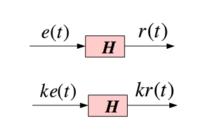圖2嚴格地說，實際的物理系統都不可能是線性系統。但是，通過近似處理和合理簡化，大量的物理系統都可在足夠準確的意義下和一定的範圍內視為線性系統進行分析。例如一個電子放大器，在小信號下就可以看作是一個線性放大器，只是在大範圍時才需要考慮其飽和特性即非線性特性。線性系統的理論比較完整，也便於套用，所以有時對非線性系統也近似地用線性系統來處理。例如在處理輸出軸上的摩擦力矩時，常將靜摩擦當作與速度成比例的粘性摩擦來處理，以便於得出一些可用來指導設計的結論。從這個意義上來說，線性系統是一類得到廣泛套用的系統。
時不變系統的定義
時不變系統是輸出不會直接隨著時間變化的系統。
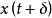線性非移變系統
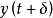線性非移變系統如果輸入信號x(t) 產生輸出 y(t)，那么對於任意時間延遲的輸入 將得到相同時間延遲的輸出 。
如果系統的傳遞函式不是時間的函式，就可以滿足這個特性。 這個特性也可以用示意圖的術語進行描述
如果一個系統是時不變的，那么系統框圖與任意延時時刻的框圖都是可以互換的。
為了表明如何確定系統是時不變系統，我們來看兩個系統如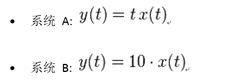圖3.
圖3由於系統 A 除了x(t)與y(t) 之外還顯式地依賴於 t 所以它是時變系統，而系統 B 沒有顯式地依賴於時間 t 所以它是時不變的。
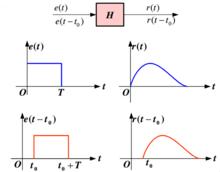圖4線性非移變系統的重要性質
線性非移變系統的三個重要性質：
1） 調諧輸入總是產生相同頻率的調諧輸出，調諧信號的實部和虛部相互獨立的通過系統。
2） 系統的傳遞函式—一個僅依賴於頻率的的復值函式，包含了系統的全部信息。
3） 傳遞函式對一調諧信號輸入只產生兩種影響—幅度的變化和相位的平移（時間原點的平移）。
