概念解釋
 維數論
維數論 維數論
維數論維數論是歐幾里得空間的維數概念的推廣。對於某些拓撲空間指定一個非負整數,稱為該空間的維數。此外,對空集 指定為-1,而對“無限維”空間指定為 。拓撲空間的維數有三種不同方式定義,即覆蓋維數(dim)、小歸納維數(inddimension theory)和大歸納維數(Ind)。它們都具有維數的特徵, 但適用的範圍不同,分別是吉洪諾夫空間、正則空間和正規空間。
概念發展
維數最初是對緊可度量化空間引入的, 其後擴張到可分可度量化空間。對於可分可度量化空間維數論的基本定理,在所有度量空間或緊空間中並不成立。因此,對於一般拓撲空間有三個維數論。龐加萊(J.H.Poincaré)於1912年略述了維數的歸納性定義。
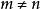 維數論
維數論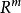 維數論
維數論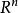 維數論
維數論維數函式的第一個精確定義是由布勞威爾(L. E. J.Brouwer)於1913年敘述的。布勞威爾的維數函式與維數Ind在局部連通緊可度量化空間中是一致的。但是布勞威爾的維數函式僅是 用來證明“若 ,則空間 與 不同胚”的一個輔助工具。
維數理論是由門格(K.Menger,)和烏雷松(ypwcon,II. C.)首創的。
ind的定義是烏雷松於1922年和門傑於1923年給出的。Ind的定義是切赫 (Cech,E.)於1931年給出的。覆蓋維數dim定義於切赫於1933年的論文中。由切赫給出的dim定義僅適用於正規空間。卡切托夫(M.Katêtov)於1950年修改了這個定義。斯米爾諾夫(M.Cmhpiiqb)於 1956年研究了另一類覆蓋導出同樣的維數函式。吉洪諾夫空間的維數論最早系統的講解是在吉爾曼 (L.Gillman)和傑里遜(M.Jerison)於 1960 年的著作中。
標準維數
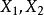 維數論
維數論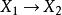 維數論
維數論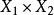 維數論
維數論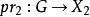 維數論
維數論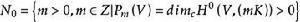 維數論
維數論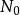 維數論
維數論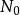 維數論
維數論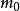 維數論
維數論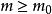 維數論
維數論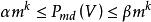 維數論
維數論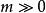 維數論
維數論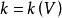 維數論
維數論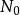 維數論
維數論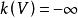 維數論
維數論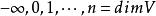 維數論
維數論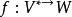 維數論
維數論設 是復簇,ψ: 是亞純映射,G⊂ 是它的圖象。如果射影 也是固有變形,則ψ叫作雙亞純映射。對於一個n維緊複流形V,我們定義V的小平維數(或標準維數)如下:設K是V的標準叢和 。如果 不空,設d是 的最大公因數,則存在一個正整數 ,正數α,β和非負整數k,對於 ,有下列不等式: ,而 。我們確定 ,如果 為空集,我們定義 。k(V)是V的一個雙亞純不變數,取下列數值之一: 。如果k(V)是正的,則存在一個複流形的纖維空間 ,使得:
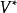 維數論
維數論(1) 雙亞純等價於V;
(2)W是維數為k(V)的非奇射影族;
(3)f是一個滿射和正常解析映射;
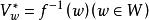 維數論
維數論(4)任意一般纖維 是不可約的;
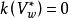 維數論
維數論(5) 。
而且這樣的纖維空間在雙亞純等價下是唯一的。
注意:小平維數(標準維數)在一般情形下不是變形的不變數。

