公式介紹
絕熱過程是在不與外界作熱量交換的條件下,系統的狀態變化過程。它的特徵是dQ= 0。要實現絕熱平衡過程,系統的外壁必須是完全絕熱的,過程也應該進行得無限緩慢。但在自然界中,完全絕熱的器壁是找不到的,理想的絕熱過程並不存在,實際的絕熱過程都是近似的。絕熱的平衡過程進行中功和能的轉換可根據熱力學第一定律(dQ= dE+ pdV)和絕熱過程的特徵方程(dQ= 0)得到。即dE+ pdV= 0,從式中看出,在絕熱過程中只有系統內能變化時才能作功。
若有m千克,M摩爾的理想氣體,當溫度升高dT時,內能增量為 dE=(m/M)CdT
於是 dA= pdV= - dE= -(m/M)CdT
因為(m/M)C是衡量,當氣體由初態T變為末態T絕熱過程中,氣體作功的絕熱方程為
A= -(m/M)C(T- T)
由式中看出,當氣體絕熱膨脹而對外作功時,氣體的內能就要減少,溫度必降低,而壓力也跟著減少。因此在絕熱過程中,氣體的P、T、V三個參量均同時改變。
根據熱力學第一定律及絕熱過程的特徵(dQ= 0),可以證明,在絕熱的平衡過程中,對於P、V、T三個參量之間,每兩個參量間的互相關係式為
PV =恆量 V T=恆量 P T =恆量
這三個方程稱為絕熱過程方程,式中γ= C/C為比熱容比。
絕熱過程
熱力學系統同外界無熱交換的過程。在良好的絕熱材料隔絕的系統中進行的過程,或由於過程進行得很快,以致同外界沒有顯著熱量交換的過程都可近似地看作絕熱過程。例如聲波在空氣中的傳播,以及內燃機中氣體的壓縮過程等,都進行得很快,可當作絕熱過程處理。 在絕熱的準靜態過程中,熱力學系統狀態參量之間存在著一定的關係,稱為絕熱過程方程。理想氣體的準靜態絕熱過程方程有以下三種形式:
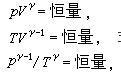 絕熱方程
絕熱方程式中γ=Cp/CV,為氣體定壓熱容同定容熱容之比,且γ>1;p、V、T 分別為氣體的壓強、體積和溫度。在p-V 圖上,經過同一點的絕熱線和等溫線二者斜率間的關係(見多方過程)為
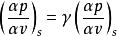 絕熱方程
絕熱方程可見在p-V 圖上的任意點處,絕熱線都比等溫線陡。 由熱力學第一定律可知,在絕熱過程(Q=0)中,能量轉換的特點是:系統內能的減少等於系統對外界所作的功,即-ΔU=A。理想氣體在準靜態絕熱過程中功的表達式為
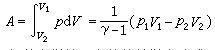 絕熱方程
絕熱方程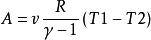 絕熱方程
絕熱方程或
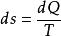 絕熱方程
絕熱方程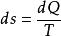 絕熱方程
絕熱方程式中v為氣體的摩爾數。 根據熱力學第二定律的數學表達式 ,可見系統的熵在可逆過程中的增量 dS 等於系統所吸收的熱量Q同熱源的熱力學溫度T 之比。對於可逆的絕熱過程而言, =0,即熵不變,所以可逆絕熱過程即等熵過程。
等溫過程
系統的溫度始終保持不變的過程。等溫過程的特點是溫度T=恆量。對理想氣體而言,在等溫的準靜態過程中,由理想氣體狀態方程得出,系統的壓強和體積的乘積保持不變,即pV=恆量。理想氣體經等溫過程由狀態I(p1,V1)到狀態 Ⅱ(p2,V2)時系統所做的功
v為氣體的摩爾數,T為氣體的熱力學溫度(見熱力學溫標),R為摩爾氣體常數。理想氣體的內能僅僅是溫度的函式,所以等溫過程中內能的變化為零。由熱力學第一定律得出,理想氣體在等溫過程中能量轉換的特點是Q=A,即系統吸收的熱量等於系統對外界所做的功。 等溫過程是熱力學中一種重要過程。卡諾循環就是由兩個等溫過程和兩個絕熱過程組成的。物質三態的可逆轉變也是在等溫條件下進行的。
絕熱過程方程導出模擬
多方過程中最具有實際意義的過程主要為等容、等壓、等溫及絕熱這四種過程.這四種過程的過程方程的建立,其難易程度相差甚遠.對等容、等壓、等溫的過程方程可直接表述為:
V=常數 P=常數 T=常數
 絕熱方程
絕熱方程以上三種過程方程的建立很直觀又極其容易,所以學生對它們沒有絲毫的疑慮.然而絕熱過程方程的建立就大不一樣了.現行的熱學教材上有二種不同的處理方法,一種是不作任何推導,直接地給出絕熱過程方程的具體形式:
PV =常數
另一種方式是依據絕熱過程的定義,如果系統在整個過程中始終不和外界交換熱量,則這種過程即為絕熱過程,得出Q=0,再使用熱力學第一定律和理想氣體的狀態方程,通過高等數學的運算,最終導出了絕熱過程方程的形式.這一推導過程屬於典型的“定義+定律+數學運算”的模式,缺少物理模型的參與,所以不能給學生留下直觀的認知,學生對方程只知其然,不知其所以然,在學生運用該公式解答習題時會產生各種各樣的疑慮,導致各種各樣錯誤的產生.為了克服這一弊端,本文採用往返於兩壁間的可視質點的彈性小球與可動壁的碰撞來模擬說明當氣體被壓縮時其溫度升高的機理,並且能在一維方向上推導出單原子氣體的結果,繼而推廣到三維和多原子氣體分子,最終模擬導出理想氣體絕熱過程方程,具體模擬推導過程如下所述;如圖1所示,在一個帶有活塞的柱形氣缸內有一單原子分子沿著氣缸的長度方向,從活塞近旁以v的初始速率朝氣缸底面運動,同時活塞以u《 v的速率向前推進.氣缸的初始長度為L,橫截面積為S,假設氣缸置於無重力場的太空中,因此不用考慮重力的影響.
如圖2所示,分子經Δt1時間與活塞第一次相碰,此時活塞推進的距離為ΔL1,則有
Lo+(Lo-△L1)=Vo△t1
△L1=u△t1
得△t1=2Lo/vo+u △L1=2Lou/vo+u
以活塞為參照系,分子與活塞相碰前的接近速度為v0+ u,因彈性碰撞,碰後分離速度大小也為v0+ u,故碰後相對固定的氣缸,分子速率為
v=v+ 2uv
為分子與活塞第一次碰撞後的分離速度,第一次相碰後,瞬間氣缸長度為L1,則有
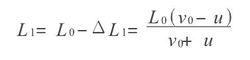 絕熱方程
絕熱方程分子又經Δt2時間與活塞第二次相碰.此時,活塞又推進ΔL2間距,同理可得
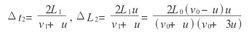 絕熱方程
絕熱方程由同樣的分析可知,第二次碰撞後分子運動速率為
v2=v1+ 2u=v0+ 4u
第二次相碰後瞬間氣缸長度為L2,則有
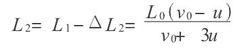 絕熱方程
絕熱方程運用數學歸納法可推知,第K-1次與第K次相碰之時間間隔為Δtk,活塞在此時間間隔內推進的間距ΔLk,第K次相碰後瞬間分子運動速度vk,此時瞬間氣缸長度Lk分別為
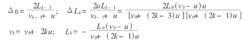 絕熱方程
絕熱方程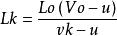 絕熱方程
絕熱方程從以上幾式即得
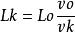 絕熱方程
絕熱方程因v0>>u, vk>>u,故有
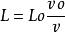 絕熱方程
絕熱方程將vk近似視為連續變化,Lk也隨之連續變化,用變數v,L替代,則有
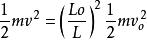 絕熱方程
絕熱方程由上式可得
其中m為分子質量.又因為V0=SL0, V=SL,所以可得
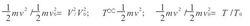 絕熱方程
絕熱方程其中T和T0分別對應動能1/2mv 和1/2mv 的兩個“溫度”.
於是有TV = TV =常數
上式為一維情況下的結果,假如構想有一個正方形容器的三個面固定,另三個面同時均稱地向三個固定面推進,那么上述過程應改寫為
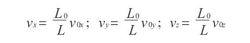 絕熱方程
絕熱方程由以上三式可得
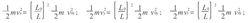 絕熱方程
絕熱方程由以上三式相加可得
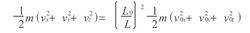 絕熱方程
絕熱方程此時體積應表示為Vo=Lo ,V=L ,所以上式即為TV =ToVo
絕熱過程方程“ PV =常數”中的指數V為Cp/Cv,CP又等於CV+ R,作為單原子氣體分子的CV為3/2R,所以當氣體為單原子分子時有
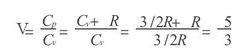 絕熱方程
絕熱方程即單原子分子氣體的絕熱過程方程應為 PV =常數, PV =PoVo
將理想氣體的狀態方程 PV/T=常數,即PV/T=PoVo/To
代入上式即可得 TV = ToVo =常數
所以上述模擬推導最終能得到 PV =常數

