納維法
正文
用雙三角級數求解薄板彎曲邊值問題的一種精確解法,是法國力學家 C.-L.-M.-H.納維於1820年提出的。納維利用它得到薄板彎曲邊值問題的第一個精確解。此法適用於求解四邊簡支的矩形薄板的彎曲邊值問題,板上作用的載荷可以是分布的或集中的。在下圖所示的坐標系中,薄板的微分方程為:,
式中w為板的撓度;p(x,y)為作用在板上的分布載荷;D為板的彎曲剛度。納維法的要點是:將載荷p(x,y)展成雙重正弦級數,即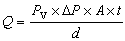
納維法是用雙三角級數求解薄板彎曲邊值問題的一種精確解法,是法國力學家 C.-L.-M.-H.納維於1820年提出的。納維法可推廣用於正交各向異性的、彈性基礎上的以及在垂直於板面和板面內載荷共同作用下的簡支邊矩形板。
,
式中w為板的撓度;p(x,y)為作用在板上的分布載荷;D為板的彎曲剛度。納維法的要點是:將載荷p(x,y)展成雙重正弦級數,即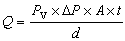
賴納·維爾納·法斯賓德(1945年5月31日—1982年6月10日),出生於巴伐利亞,德國導演、編劇、製片人、演員。 1965年,執導個人首部劇情短片《...
早年經歷 演藝經歷 個人生活 主要作品 獲獎記錄維爾納·法伊曼(Werner Faymann),曾任奧地利總理。1960年5月4日出生於奧地利首都維也納,法律專業畢業。他先後任奧“社會主義青年”維也納...
競選過程 個人生活 辭職訊息在此處,“映像”替代在電影誕生之初的放映機投射影像的感知與印象。 《映像館》是系統梳理當代電影大師作品與創作的一套系列叢書。 《映像館》的產生緣於少數人...
內容介紹納爾維克海戰,1940年4月挪威戰役期間的一次海戰。1940年4月13日,第二次納爾維克海戰爆發。
簡介 起因 德軍占領納爾維克 第一次海戰 第二次海戰本詞條尚需完善,如需幫助請參見:互動百科:詞條標準
賴納·維爾納·法斯賓德(1945年5月31日—1982年6月10日),出生於巴伐利亞,德國導演、編劇、製片人、演員。 1965年,執導個人首部劇情短片《...
早年經歷 演藝經歷 個人生活 主要作品 獲獎記錄法比奧·卡納瓦羅(Fabio Cannavaro),1973年9月13日出生於義大利那不勒斯,義大利前職業足球運動員、教練,司職後衛,擔任廣州恆大淘寶足...
早年經歷 運動生涯 教練生涯 場外生活 獲獎記錄納維克戰役:坐落在北極圈內的挪威的港口小鎮納維克(Narvik)在1940年4月9日-6月8日期間見證了一場驚心動魄的戰役。盟軍方面,以英軍為主力,再加...
起因 德軍占領納維克和兩次烏夫特峽灣海戰 德軍的危難時刻 盟軍進攻納維克 撤退及以後