面積積分
正文
假設ƒ(z)是單位圓|z|<1內的解析函式,ƒ┡(z)是它的導數,那么積分 (1)
(1)
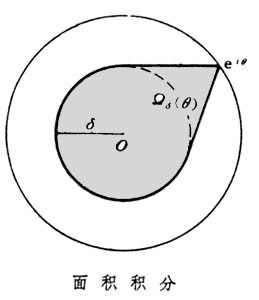 ),這裡δ是小於1的某個正數,Ωδ(θ)是由點eiθ引圓周Cδ(│z│=δ)的兩條切線與Cδ上被兩切點所截的、離eiθ較遠的圓弧所圍的區域。
),這裡δ是小於1的某個正數,Ωδ(θ)是由點eiθ引圓周Cδ(│z│=δ)的兩條切線與Cδ上被兩切點所截的、離eiθ較遠的圓弧所圍的區域。 積分(1)中的被積函式
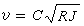 是映射z→ƒ(z)的雅可比行列式,當ƒ(z)為一一映射時,可知(Sδ(ƒ)(θ))2正好是區域Ωδ(θ)在映射ƒ下的映像面積。面積積分的名字由此而來。
是映射z→ƒ(z)的雅可比行列式,當ƒ(z)為一一映射時,可知(Sδ(ƒ)(θ))2正好是區域Ωδ(θ)在映射ƒ下的映像面積。面積積分的名字由此而來。 Sδ(ƒ)(θ)在某些點eiθ處,可能是無限的。但是,盧津為了研究一類解析函式的性質,證明了當 ƒ(z)∈h2,即
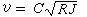
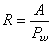 , (2)
, (2)
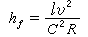 , (3)
, (3)
後來,J.馬欽凱維奇和A.贊格蒙把上述定理又推廣到函式類hp(p>0),即滿足條件

面積積分的重要性,還在於它本質上可以局部地刻畫圓內解析函式ƒ 在邊界z=eiθ 處非切向極限的存在性。確切地說,除了一零測度集外,圓內解析函式ƒ 在邊界z=eiθ處具有非切向極限的充分必要條件是
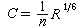 。
。

