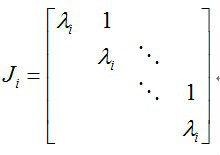約當塊

約當標準型的對角元素為約當塊。

如果一個矩陣能夠寫成如下的形式，我們就稱其為約當標準型（Jordan normal form），記號為J。

在約當標準型對角線上的分塊矩陣Ji，稱為約當塊（Jordan block）。

約當塊的對角元素為矩陣的特徵值，對角線的上斜線元素全部為1。

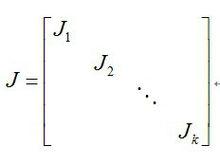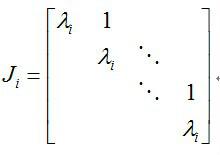約當塊

約當塊

現代控制論

約當標準型可以用於判定線性定常連續系統是否狀態完全可控，狀態完全能觀。

設系統狀態方程為 X'=AX+BU Y=CX+DU

系統完全可控的判據是：

1、若矩陣A（系統矩陣）的特徵值是兩兩相異的，則可將A進行線性變換為 對角矩陣A1 。此時對應的B矩陣（輸入矩陣）變換為B1。若B1陣不包含元素全為0元素的行，則該系統一定是完全可控的。

系統完全能觀的判據是：

1、若矩陣A（系統矩陣）的特徵值是兩兩相異的，則可將A進行線性變換為 對角矩陣A1 。此時對應的C矩陣（輸出矩陣）變換為C1。若C1陣不包含元素全為0元素的列，則該系統一定是完全能觀的。